17. Функция распределения одномерной случайной величины, определение, доказательства свойств (включая формулу вероятности попадания в промежуток).

Функцией распределения F(x) случайной величины ξ называется вероятность того, что случайная величина ξ в результате испытания примет значение, меньшее х, т.е.

F(x)=P(ξ<x).

Свойства F(x):

1) Область определения f(X) - интервал

2) 0 < F(x) £ 1,

3) F(-¥)=0, т.к. P(ξ<- ¥)=P(Ø)=0,

4) F(+¥)=1, т.к. P(ξ<+ ¥)=P(W)=1,

5) F(X)- неубывающая функция.

Будем считать, что F(x) непрерывна слева

Вероятность попадания случайной величины в промежуток и в точку

Основное свойство функции распределения

Р(a £ ξ < b)=F(b) – F(a).

Вероятность попадания случайной величины в заданный интервал равна разности значений функции распределения в концах интервала

Следствие:

Р(ξ=a) =

Действительно:

Замечание

Функция распределения случайной величины ξ

F(x)=

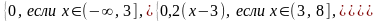
Найти вероятность попадания случайной величины ξ в интервал (1;6).

Решение Р(1<ξ<6)=F(6)-F(1)=0,2(6-3)-0=0,6.4

18. Дисперсия и среднеквадратическое отклонение случайной величины, формула для дискретного распределения, доказательство свойств дисперсии.

Дисперсией D(ξ) случайной величины ξ называется математическое ожидание квадрата ее отклонения от математического ожидания:

Среднее квадратическое отклонение

Свойства дисперсии

1. D(C) = 0

2. D(kξ) = k²D(ξ)

3. D(ξ) = M(ξ²) – [M(ξ)]²

Пример:

D(ξ) = 13,61

D(η) = 4,17

Основные распределения дискретной случайной величины

• Вырожденное распределение

• Распределение Бернулли

• Дискретное равномерное распределение

• Биномиальное распределение Р_n(m) = C_n^m p ^mq^{n -m}, где m=0;1;2;...,n и q=1-p.

• Гипергеометрическое распределение

• Геометрическое распределение

• Распределение Пуассона

19. Биномиальное распределение. Формула вероятности, интерпретация, математическое ожидание с выводом, дисперсия.

Биномиальное распределение

Биномиальным распределением называется распределение дискретной случайной величины ξ = m, для которой ряд распределения задается формулой Бернулли

где m=0;1;2;...,n и q=1–p.

Биномиальное распределение имеет дискретная случайная величина ξ – число появлений события А в n независимых испытаниях, если вероятность появления события А в каждом испытании постоянна и равна р, и, следовательно, вероятность непоявления события А в каждом испытании равна q=1–p.

Числовые характеристики биномиального распределения

Пусть _i – случайная величина, равная 1, если i-тое испытание завершилось успехом и 0 – в противном случае. Тогда каждое _i имеет следующее распределение

Сумма всех _i равна числу успехов в схеме Бернулли, т.е.

= ₁+…+ _n. Поэтому M = M(₁+…+ _n) = M₁+…+ M_n.

Для каждого _i имеем M_i = 0q + 1p = p. Отсюда

M = M₁+…+ M_n = p +…+ p = np.

Аналогично для дисперсии получаем

D = D(₁+…+ _n) = D₁+…+ D_n.

D_i = (0–p)²q + (1–p)² p = p²q+q²p = pq(p+q) = pq.

D = D₁+…+ D_n = pq +…+ pq = npq.

Вывод математического ожидания и дисперсии

Пример . Случайная величина ξ – число бракованных деталей из возвратной выборки в 400 штук. Вероятность брака одной детали р=0,1. Найти Mξ, Dξ, _ξ.

Решение.

Случайная величина ξ имеет биномиальное распределение, следовательно,

Mξ = np = 4000,1 = 40, Dξ = npq = 4000,1(1-0,1) = 36,