39. Точечные оценки параметров распределения, выборочное среднее, выборочная дисперсия, исправленная дисперсия, метод моментов.

Групповая и общая средние

Допустим, что некоторая совокупность разбита на несколько непересекающихся групп, необязательно одинаковых по объему. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе. Рассматривая каждую группу как самостоятельную совокупность, можно найти их среднюю арифметическую.

Групповой средней называют среднее арифмети-ческое значений членов, принадлежащих группе.

Общей средней всей совокупности называют среднее арифметическое значений членов, принадлежащих всей совокупности.

Справедливо предложение:

общая средняя равна средней арифметической групповых средних всех непересекающихся групп.

Пример. Вычислить среднее число жителей в поселках городского типа по данным таблицы

(21039 + 4976 +7,51251 + 15422 + 2551)/3739=6,14 (тыс. чел.)

Пример . Распределение рабочих предприятия по заработной плате и по цехам приведено в таблице. Найти среднюю зарплату.

Решение.1 способ

Оценка дисперсии

В качестве оценки D_ξ можно взять распределения выборочную дисперсию

Можно доказать, что выборочная дисперсия является состоятельной и смещенной оценкой генеральной дисперсии D_ξ, причем ,

т.е. эта оценка занижает в среднем истинное значение дисперсии на D_ξ /n. Правда это смещение сходит на нет при n  .

С целью исправления смещения вводят несмещенную оценку D_ξ, которой является исправленная выборочная дисперсия

Действительно

Так как , то оценка s² является несмещенной.

Итак

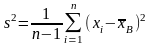
Стандартно вводятся выборочное среднее квадратическое отклонение

и исправленное среднее квадратическое отклонение

Замечания:

• На практике пользуются исправленной дисперсией, если n30.

• Если, x_i – варианта выборки, n_i – ее частота и n – объем выборки, то

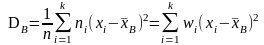
• Для вычисления D_В удобнее применять формулу

• Выборочное _в и исправленное s (средние квадратические отклонения) – смещенные оценки .

• Пример. Из генеральной совокупности извлечена выборка

Найти несмещенные оценки генеральной средней и генеральной дисперсии

Решение.

Объем выборки n = 2 + 5 + 3 = 10,

или

40) Интервальные оценки, доверительный интервал, вывод доверительного интервала для параметра a нормальной случайной величины нормального распределения при известном σ

Точность, надежность. Доверительный интервал

При небольшом объеме выборки точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводит к грубым ошибкам. По этой причине при малом объеме выборке следует пользоваться интервальными оценками, которые позволяют установить точность и надежность оценок.

Пусть по выборке (x_1, x₂,..., x_n) найдена каким-то методом несмещенная точечная оценка

неизвестного параметра q.

Зная закон распределения точечной оценки q^*, можно для заданной вероятности g (близкой к единице)

найти такой интервал (q₁,q₂) со случайными границами q₁ и q₂, что P(q₁<q^*<q₂) =g. Длина интервала q₂–q₁ характеризует точность оценки q^*, а число g называют доверительной вероятностью или надежностью этой оценки.

Равенство P(q₁<q<q₂)=g означает, что интервал (q₁,q₂) покрывает неизвестный параметр q с вероятностью g.

Интервал (q₁,q₂) со случайными границами q₁ и q₂, покрывающий параметр q с заданной вероятностью g, называется доверительным интервалом и является интервальной оценкой параметра q.

Предположим, что параметр   неизвестен, а дисперсия   -- известное фиксированное число. Пусть   -- доверительная вероятность. Применим метод, изложенный в   8.1. Выберем функцию

Из Упражнения 4.7 вытекает, что   имеет нормальное распределение. Нетрудно видеть, что это стандартное нормальное распределение  . Следовательно,  . Выбирая 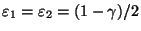  и  ,  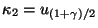, заключаем, что неравенство

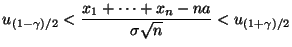
выполнено с вероятностью  . Решая его, находим доверительный интервал:

Если теперь заметить, что  , то  -доверительный интервал можно записать еще проще: