1.Определение числовой последовательности.
Если каждому значению п натурального ряда чисел 1, 2, ... ..., п, ...
ставится в соответствие по определенному закону некоторое веще-
ственное число хп, то множество занумерованных вещественных чисел х1, х2, х3, .... хn, ...
мы и будем называть ч и с л о в о й п о с л е д о в а т е л ь н о с т ь ю или просто п о с л е д о в а т е л ь н о с т ь ю .
Пример 1.
Таким образом, получаем последовательность
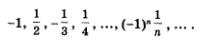
Пример 5.
1, 3, 5, 7, 9, ... . Здесь уn = 2n - 1 (последовательность нечетных чисел).
Пример 6.
2, 4, 6, 8,10, ... . Здесь уn = 2n (последовательность четных чисел).
2. Определение предела числовой последовательности. число а называется пределом числовой последовательности аn, если для любого сколь угодно малого числа ε>0, найдётся натуральный номер N такой, что для всех чисел n³ N выполняется модуль раз-
ности |an-a|<ε Û " ε>0 $ N: " n³ N Þ|an-a|<ε.
Обозначается: Lim an=а
Начиная с этого номера N, все числа этой последовательности попада-
ют в ε окрестность числа а. Другими словами, начиная с номера N вне интервала а-ε;а+ε, может находиться не более конечного числа членов последовательности.
Пример . Найтн предел последовательности:
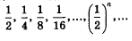
Решение. Здесь, как и в предыдущем примере, последовательность сходится к 0:
Результат: полученный
в примере 2, является частным случаем
более общего утверждения:
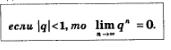А
что будет с последовательностью
Пусть,
например, q =2, т.е. речь идет о
последовательности 2, 22,
23,
24,
..., 22,
... Эта последовательность явно не имеет
предела (нет «точки сгущения»). Вообще,
справедливо утверждение:
3. Понятие бесконечно малой и бесконечно большой числовой последовательности.
Связь между ними.
Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
4. Св-ва пределов числовых последовательностей. Доказать второй замечательный предел. Свойства числовых последовательностей.
Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.
Определение. Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < ….
Определение. Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y1 > y2 > y3 > … > yn > yn+1 > … .
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Пример 1. y1 = 1; yn = n2\shad \shad0– возрастающая последовательность.
Пример
2. y1
= 1;
–
убывающая последовательность.
Пример
3. y1
= 1;
–
эта последовательность не является не
возрастающей не убывающей.
Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство yn = yn+T . Число T называется длиной периода.
Пример.
Последовательность
периодична
с длиной периода T=
2.
Доказать второй замечательный предел.
Вторым замечательным пределом называется предел
Теорема 2.15 Второй
замечательный предел существует. Его
значение 
--
число, лежащее между 
и 
.
Более подробное изучение числа показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:
Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона
Доказательство теоремы
2.15.
Рассмотрим последовательность 
и
применим к 
формулу
бинома Ньютона при 
и 
.
Получим
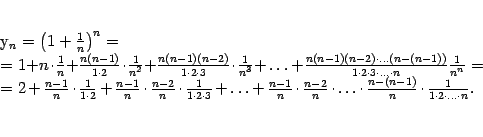
Покажем,
что последовательность
ограничена
сверху. Для этого заменим все дроби 
, 
,
..., 
на
1. Все эти дроби меньше 1, так что сумма
в правой части формулы
5. Дать определение эквивалентных бесконечно малых функций. Использование эквивалентности для вычисления пределов.
Б.м.
функции 
и 
называются эквивалентными или равносильными
б.м. одного порядка при 
,
если 
Обозначают: 
при
.
Использование эквивалентности для вычисления пределов.
Предел
отношения двух б.м. функций
и
при
равен
пределу отношения эквивалентных им
б.м. функций 
и 
при
,
то есть верны предельные равенства:
