Предельный переход в функциональных неравенствах.
Теорема о
предельном переходе в
неравенстве. Пусть 
\\ 
тогда
Доказательство. (от противного)
Пусть 
.
-
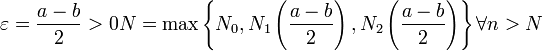
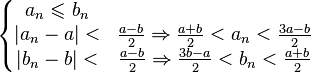
противоречие.
Непрерывность функции в точке. Определения непрерывности по Гейне и по Коши. Непрерывность функции в точке слева и справа. Локальные свойства непрерывных функций: ограниченность, сохранение знака.
Определение:
Функция 
,
определенная в некоторой окрестности точки
,
называется непрерывной, если 
Определение(по Коши):
Определение (по Гейне):
Определение:
Функция
непрерывна , если 
,
то есть бесконечно маломуприращению
аргумента соответствует
бесконечно малое приращение
функции.
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
|
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
Элементарные функции. Непрерывность простейших элементарных функций. Примеры.
Арифметические операции над непрерывными функциями. Суперпозиция функций. Теорема о непрерывности сложной функции.
Точки разрыва функции. Их классификация. Примеры.
Непрерывность функции на множестве. Свойства функций, непрерывных на отрезке: теоремы о прохождении функции через нуль и через промежуточное значение.
Теоремы об ограниченности функции, непрерывной на отрезке (1-я теорема Вейерштрасса) и о достижении такой функцией точных верхней и нижней граней ее значений (2-я теорема Вейерштрасса).
Производства функции. Физический и геометрический смысл производной функции. Правая и левая производные функции в точке. Связь дифференцируемости и непрерывности функции в точке.
Дифференцирование сложной функции и обратной функции. Производные суммы, разности, произведения и частного двух функций.
Формулы дифференцирования простейших элементарных функций. Примеры.
Теорема о нуле производной (теорема Ролля).
Теорема Лагранжа (формула конечных приращений).
Теорема Коши )обобщенная формула конечных приращений).