Фундаментальная последовательность и ее свойства. Критерий Коши сходимости числовой последовательности. Примеры применения критерия Коши.
Определения Править
Пусть дано метрическое пространство
,
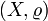а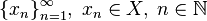 
является последовательностью элементов 
.
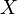Тогда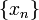 
называется
фундаментальной или последовательностью
Коши, если
Свойства Править
Любая последовательность, имеющая предел, является фундаментальной.Критерий Коши для сходимости функциий : Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
Если фундаментальная последовательность содержит сходящуюся подпоследовательность
,
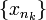то она сама сходится.
Пусть
задана числовая последовательность
{xn}.
Эта последовательность сходится тогда
и только тогда, когда для любого числа ε >
0 существует номер N такой,
что при всех n > N и
любых натуральных m выполняется
неравенство 
(т.е.
расстояние между членами последовательности
с номерами n и n+m меньшеε)
– критерий
Коши сходимости
последовательности.
Пример 1
Рассмотрим
последовательность с общим членом 
Найдем
модуль разности между её n-м
членом, хn,
и (n+m)-м
членом, xn+m:
Если
для любого ε >
0 положить 
,
то при всех n > N и
любых натуральных mиз
наших выкладок следует, что 
Итак, взятая последовательность удовлетворяет критерию Коши, поэтому она сходится (имеет предел).
Поскольку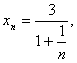 
а
дробь в знаменателе при n →∞
стремится к нулю, её предел равен 3.
Также отметим, что последовательность, удовлетворяющая критерию сходимости Коши, называется также фундаментальной или последовательностью Коши.
Понятие фундаментальной последовательности важно также в любом метрическом пространстве. В частности, если любая фундаментальная последовательность в метрическом пространстве сходится к элементу этого же пространства, такое пространство называется полным. Таким является, например, одномерное пространство действительных чисел (всех точек числовой прямой), но не является множество Q рациональных чисел.
Два определения предела (предельного значения) функции: по Гейне и по Коши, их эквивалентность. Единственность предела функции в данной точке. Односторонние пределы. Бесконечные пределы и пределы на бесконечности.
Пусть f: X → R и x0 - предельная точка множества X.
(Гейне):
Функция f имеет предельное
значение при x → x0 (или
в точке x0),
если существует такое число 
,
что для произвольной последовательности
(xn)
значений 
,
сходящейся к точке x0,
соответствующая последовательность
значений функции (f(xn))
сходится к точке A.
(Коши): Функция f имеет предел при x → x0, если
При этом число A называем пределом (или предельным значением) функции f в точке x0 и записываем
или f(x)
→ A при x → x0.
Определение Гейне и Коши эквивалентны.
Введем понятие одностороннего предела.
(Гейне): Функция f имеет в точке x0 предел слева (справа), если существует такое число , что для произвольной последовательности (xn) значений x, a < xn < x0 (x0 < xn < b), сходящейся к точке x0 при n → ∞, соответствующая последовательность (f(xn)) значений функции f сходится к точке A.
(Коши): Функция f имеет в точке x0 предел слева (справа), если
Теорема о единственности предела
Формулировка:
Если
функция 
в
точке 
имеет
предел, то этот предел единственный.
Доказательство:
Докажем
методом от противного. Предположим,
что 
, 
, 
.
Возьмём 
,
по определению и свойству окрестности
найдётся такая проколотая 
-окрестность
точки
(
),
в которой одновременно будут выполнятся
неравенства 
, 
,
тогда в точках этой же окрестности 
. Получили
противоречие 
.
Отсюда, функция
в
точке
имеет
единственный предел.
Пусть
переменная x
стремится к a,
оставаясь больше a,
и при этом 
.
Тогда число A
называют правосторонним
пределом (или пределом
справа)
функции 
и обозначают любым из символических
выражений
Понятие
левостороннего предела (или предела
слева) вводится аналогичным образом. В
этом случае 
при x → a
со стороны меньших значений:
Для существования обычного (двустороннего) предела функции в точке a необходимо и достаточно равенство между собой односторонних пределов:
Например, в точке x = 3 односторонние пределы функции
отличаются друг от друга:
Поэтому в рассматриваемой точке предел функции не существует.
Бесконечные пределы в конечной точке
Проколотой
окрестностью точки
называется 
Говорят,
что функция
,
определенная в некоторой проколотой
окрестности точки
имеет бесконечный предел в
этой точке, если
(1)
и
пишут, что 
.
В этом случае функцию называют бесконечно
большойпри 
.
Данный общий случай можно разделить на
два частных: 
,когда
в условии (1) 
и,
соответственно, 
,когда
в условии (1) 
.
Пример
Рассмотрим
поведение функции 
в
окрестности точки 
Функция
определена на всей вещественной оси
кроме т.
.
Рассмотрим некоторую проколотую
окрестность 
.
Как видно, для 
такое,
что 
.
Отсюда, по определению, следует, что эта
функция бесконечно большая при 
.
При этом на 
,
а на 
.
Пределы в бесконечности
Число
называется пределом
функции
на
бесконечности (записывается
)
если
Отсюда,
очевидно, следуют определения предела
на 
и
на
.
Абсолютно
аналогично определяется бесконечный
предел в бесконечности на
и
на
Пример
Рассмотрим
функцию 
При 
значение
функции монотонно
растет.
Для любого
и
соответствующего ему
найдется
такой 
,
например, 
,
что 
.
Иначе говоря, 
.
Что равносильно утверждению 
.
Первый и второй замечательные пределы. Следствия из них. Примеры использования.
Определение 2.11 Первым замечательным пределом называется предел
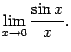
Теорема 2.14 Первый
замечательный предел равен 
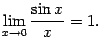
Доказательство.
Рассмотрим два односторонних
предела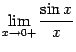 
и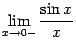 
и
докажем, что каждый из них равен 1. Тогда
по теореме
2.1 двусторонний
предел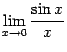 
также
будет равняться 1.
Итак,
пусть 
(этот
интервал -- одно из окончаний базы 
).
В тригонометрическом круге (радиуса 
)
с центром 
построим
центральный угол, равный 
,
и проведём вертикальную касательную в
точке 
пересечения
горизонтальной оси с окружностью (
).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой 
,
а с вертикальной касательной --
буквой 
;
через 
обозначим
проекцию точки
на
горизонтальную ось.
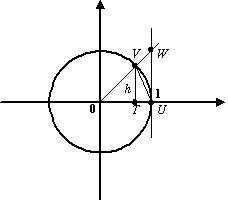
Рис.2.27.Тригонометрический круг
Пусть 
--
площадь треугольника 
, 
--
площадь кругового сектора
,
а 
--
площадь треугольника 
.
Тогда очевидно следующее неравенство:
Заметим,
что горизонтальная координата
точки
равна 
,
а вертикальная -- 
(это
высота треугольника
),
так что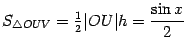 
.
Площадь центрального сектора круга
радиуса 
с
центральным углом
равна 
,
так что 
.
Из треугольника
находим,
что 
.
Поэтому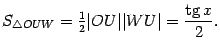 
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
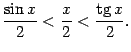
Все три части этого неравенства положительны, поэтому его можно записать так:
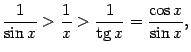
или
(умножив на 
)
так:
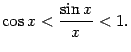
Предел
постоянной 1 в правой части неравенства,
очевидно, равен 1. Если мы покажем, что
при
предел 
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части 
также
будет равен 1.
Итак,
осталось доказать, что 
.
Сперва заметим, что 
,
так как
равняется
длине дуги окружности 
,
которая, очевидно, длиннее хорды 
.
Применяя теорему "о двух милиционерах"
к неравенству
при , получаем, что
|
(2.3) |
Простая
замена переменной 
показывает,
что и 
.
Теперь заметим, что 
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
|
(2.4) |
Тем самым показано, что
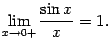
Сделаем
теперь замену 
;
при этом база
перейдёт
в базу 
(что
означает, что если 
,
то 
).
Значит,
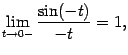
но 
(
--
нечётная функция), и поэтому
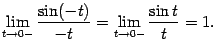
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.
Доказанная
теорема означает, что график
функции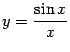 
выглядит
так:
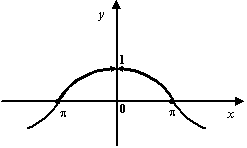
Рис.2.28.График
Приведём примеры применения первого замечательного предела для вычисления других родственных пределов.
Пример 2.18
Вычислим предел 
.
Очевидно, что
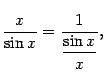
при этом предел знаменателя -- это первый замечательный предел, равный 1 (и, следовательно, не равный 0). Числитель правой части, равный 1, имеет предел 1. Значит, по теореме о пределе отношения,
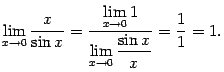
Второй замечательный предел[править | править исходный текст]
или 
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что 
.
Рассмотрим два случая:
1.
Пусть 
.
Каждое значение x заключено между двумя
положительными целыми числами: 
,
где 
—
это целая часть x.
Отсюда
следует: 
,
поэтому
.
Если
,
то 
.
Поэтому, согласно пределу 
,
имеем:
.
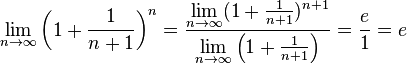
По
признаку (о пределе промежуточной
функции) существования пределов 
.
2.
Пусть 
.
Сделаем подстановку 
,
тогда
.
Из
двух этих случаев вытекает, что
для
вещественного x. 
Следствия
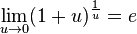
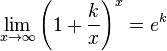
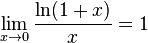
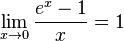
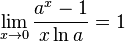для 
, 
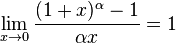
Пример 2.23
Найдём предел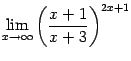 
.
Здесь основание степени имеет предел
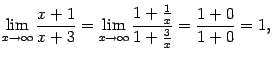
а
показатель степени 
.
Поэтому можно применять тот же приём
сведения ко второму замечательному
пределу, что в предыдущем примере. Для
начала найдём, что следует взять за
бесконечно малую величину 
.
Поскольку основание степени стремится
к 1, то оно равно 
,
где 
(см. теорему
2.4).
Значит,
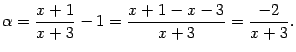
Теперь преобразуем функцию, стоящую под знаком предела:
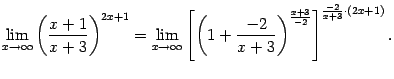
Выражение,
стоящее в квадратных скобках, имеет
вид 
и
при
стремится
к числу 
(это
второй замечательный предел), а предел
показателя степени мы найдём отдельно:
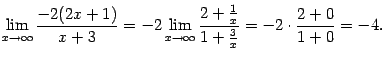
Поэтому
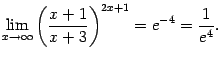
(Мы
воспользовались тем, что если 
и 
,
то 
.
Это следует из непрерывности показательной
и логарифмической функций, если учесть,
что 
.)
Арифметические операции над функциями, имеющими пределы.
Теорема
4.2. Пусть
функции 
и 
имеют
в точке 
пределы
и эти пределы соответственно равны 
и 
.
Тогда функции 
, 
имеют
в точке
пределы,
равные соответственно 
Если
кроме этого, 
,
то в точке
существует
предел функции
равный 
.
Доказательство. Пусть 
-
произвольная сходящаяся к
последовательность
значений аргумента, элементы которой
отличны от
.
Тогда последовательности 
и 
сходятся
соответственно к пределам
и
.
Но тогда, в силу теоремы 3.7,
последовательности
и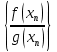 
(при
)
имеют пределы, соответственно равные 
и
.
Последнее утверждение, в силу определения
предела функции по Гейне, означает,
что 
, 
, 
.
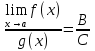Теорема 4.2 доказана.
Теорема
4.3. Пусть
функции 
и 
определены
в некоторой окрестности точки
,
за исключением, быть может, самой
точки
и
имеют в этой точке равные пределы. Пусть
кроме этого выполняются неравенства 
.
Тогда существует 
при
этом 
.
Доказательство. Пусть 
-
произвольная, сходящаяся
к
последовательность,
элементы которой отличны от
.
Тогда соответствующие
последовательности
и 
имеют
предел, и эти пределы равны. Из условия
теоремы следует, что 
.
Тогда согласно теореме 3.9 
Следовательно,
существует и 
и
при этом
.
Теорема 4.3 доказана.
25.Теорема
3.8. (о
предельном переходе в неравенствах).
Если элементы сходящейся последовательности
,
начиная с некоторого номера, удовлетворяют
неравенству 
,
то и предел
этой
последовательности удовлетворяет
неравенству 
.
Доказательство. Пусть
все элементы 
,
начиная с некоторого номера, удовлетворяют
неравенству
.
Докажем, что
.
Предположим обратное, т.е. 
.
Рассмотрим положительное число 
.
Для этого числа существует номер 
такой,
что для всех 
верно
неравенство 
.
Раскрывая модуль, получим 
.
Из правого неравенства следует 
.
Последнее
неравенство противоречит условию
теоремы. Теорема 3.8 доказана.
Следствие
1. Если
элементы сходящихся последовательностей
и 
,
начиная с некоторого номера, удовлетворяют
неравенству 
,
то их пределы удовлетворяют
неравенству
Действительно,
рассмотрим последовательность 
.
Из условия имеем, что начиная с некоторого
номера, члены последовательности
неотрицательны, т.е. 
.
Тогда из теоремы 3.8 следует, что 
.
Т.е. 
.
Следствие 1 доказано.