27.Прямая геодезическая задача. Приращение координат, знаки, приращений координат.

Положение любой точки на плоскости определяется её координатами. Для определения координат последующих точек при известных координатах начальной точки известных расстояний и известных дирекционных углов решается прямая геодезическая задача. Величины 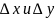называется приращениями координат.

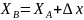
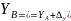, где

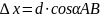
В зависимости от того в какой четверти находятся приращения координат, они будут иметь следующие знаки:

При строительстве надо определять координаты не одной точки, а целого ряда связанного между собой ………… и дирекционными углами сторон. Ряд таких точек образуют замкнутые полигоны или разомкнутые ходы.

28.Уравновешивание приращений координат в замкнутом полигоне. Абсолютная и относительная невязка в периметре полигона.

Для замкнутого полигона теоретическая сумма углов: 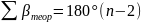, где 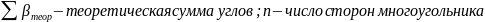. Вследствие неизбежных погрешностей практическая сумма измеренных углов 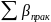отличается от теоретической суммы на величину угловой невязки . Если полученная угловая невязка 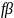не превышает допустимой вычисляемой по формуле 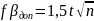, То её распределяют с обратным знаком поровну на все измеренные углы, т.е. вводят поправки в измеренные значения углов.

Абсолютная невязка в периметре полигона определяется..

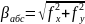
Относительная невязка

Разность между теоретическими величинами и практическими наз - невязка.

В замкнутом полигоне суммы приращений должны быть равны 0

Для теодолитного хода не должны ………

29.Обратная геодезическая задача.

Если известны координаты двух точек B’ и A, т.е. известны приращения координат по стороне АВ’, то тангенс дирекционного угла стороны АВ’ определяется из треугольника АВ”B’:

Из формулы можно написать:

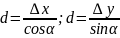
При решении обратных геодезических задач пользуются пятизначными таблицами логарифмов. Для определения величины дирекционного угла четверть устанавливают по знакам приращений координат.

План теодолитного хода

Определяем координаты вершин зд.

Выписываем из ведомости координат вершин полигона

Определяем прирощения координат

Определяем tg румбов линии

По знаком прирощения находим в какой четверти расположены линии

Определяем азимуты румбов

определяем углы

30.Координатная сетка, её построение.

Предварительно на бумаге строят координатную сетку квадратов со сторонами, равными 10 см. Общие размеры координатной сетки зависит от величины разностей наибольших и наименьших значений координат наносимых точек. При построении координатной сетки линейкой Дробышева кладут параллельно нижнему краю листа бумаги. По скошенному краю прочерчивают линию и, сместив линейку так, чтобы черта прошла по середине отверстий, по скосам вырезов проводят чёрточки-засечки, получая точки 1,2,3,4,5,6. Затем перекладывают линейку под углом 90 в направлении ВС и прочерчивают засечку по скошенному ребру шестого отверстия. Далее кладут линейку по диагонали АС, совмещая штрих на скосе нижнего окошечка с начальной точкой А/f и по скошенному торцу линейки прочерчивают засечку, пересекающую засечку при точку С. Полученная точка пересечения определяет положение верхней правой вершины квадрата. Аналогично получают верхнюю левую вершину квадрата.

31.Построение точек по координатам и графическое определение координат точек по координатной сетке.

Чтобы нанести на чертёж точку по координатам, отыскивают квадрат сетки, в котором содержатся координаты наносимой точки. Найдя нужный квадрат, откладывают в принятом масштабе величину Х с одной и с другой сторон данного дециметрового квадрата. После этого откладывают величину У по верхнему и нижнему основаниям дециметрового квадрата. Соединяют отложенные величины Х и У. В месте пересечения линий будет находиться искомая точка.

Наложенные по координатам точки слегка накладывают и обводят кружком минимального градуса. Правильность нанесения точек по координатам проверяют по расстояниям между соседними точками, выбираем из «координатной ведомости».

32.Определение угловой невязки в замкнутом полигоне. Допустимость угловойугловой невязки и распределение в замкнутом полигоне.

В замкнутом полигоне угловая невязка равна.

Допустима угловая невязка: 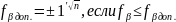Её распределяют поровну на все станции с обратным знаком. После уравновешивания сумма измеренных углов должна равняться теоритической.

Невязки обозначают f_x f_y

33Последовательность обработки координатной ведомости замкнутого теодолитного хода.

1)дерекционный угол строительного полигона

2)внутренние углы полигона

3)горизонтальные проложение линий

4)координаты начальных точек

Порядок отсчета

4.1Определяем сумму измеренных углов

4.2Определяем теоритическую сумму углов

4.3Определяем угловую невязку

4.4Определяем допустимую угловую невязку

4.5Наводим поправку, получаем значение исрправленных углов

5)Определяем дерекционные углы всех линий

Потом выполняем проверку

6)Определяем румбы

7)Вычисляем прирощение координат

8)Определяем сумму прирощений находим линейные невязки f_x- f_y

9)Определяем абсолютную невязку

10)определяем относительную невязку

11)определим исправленные прирощения, находим их сумму.

Определим координаты точек

Выполняем проверку

34Вычисления координат точек замкнутого теодолитного хода.

В замкнутом теодолитном ходе обычно измеряют внутренние углы полигона . Необходимость привязки замкнутого хода к двум твердым линиям связана с тем, что при ошибочном опознавании, например пункта А, дирекционный угол линии АН не будет соответствовать его действительному значению и весь полигон будет неправильно ориентирован относительно принятой системы координат. Поэтому для исключения такой ошибки необходимо делать привязку хода как минимум к двум опорным линиям. Внутри замкнутого хода можно проложить диагональный ход, опирающийся на вершины основного хода Последовательность обработки замкнутого хода такая же как и разомкнутого. Но исходными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. Это накладывает на обработку замкнутого хода следующие особенности.

Угловая невязка вычисляется по формуле, в которой в отличие от разомкнутого хода

,

где n – число углов в полигоне.

После распределения угловой невязки и вычисления дирекционных углов сторон хода контролируют правильность вычислений - в конце должно быть получено то же значение дирекционного угла, которое было исходным.

Невязки в координатах находят по формулам:

,  .

Эти соотношения следуют из формул (6.3), где в данном случае  ,  . Распределив невязки f_x и f_y и вычислив координаты точек хода, контролируют правильность вычислений - вычисленные в конце координаты начальной точки хода должны равняться исходным.