1 билет

Основные этапы становления математики

Математика – наука о количественных отношениях и пространственных формах действительного мира. Академик Колмогоров А. Н. выделяет 4 периода развития математики:

Зарождение

Элементарная математика

Математика переменных величин

Современная математика

Начало периода элементарной математики относят к 6-5 вв. до н. э Развивается арифметика,появляется теория чисел. Создается алгебра. В 17 в. Вопросы естесствознания и техники привели к созданию методов позволяющих математически изучать движение, изменение величин, преобразование геометрических фигур. Начинается период математики переменных величин. Великими открытиями 17в. Является введенная Ньютоном и Лейбницем понятие бесконечно малой величины и создание математического анализа. Возникают новые теории. Развитие математики 19-20 вв. позволяет отнести ее к современной математики. В основе построения мат теории лежит аксиомотический метод. Основа метода математических исследований – математические доказательства, строгие логические рассуждения

Начала Евклида как образец аксиоматического построения научной теории.

Образцом аксиоматического построения математической науки является элементарная геометрия. Система аксиом геометрии была изложена Евклидом. Элементарная геометрия имеет 13 аксиом, которые разбиты на 5 групп. В 5 группе – одна аксиома о параллельных прямых (5 постулат Евклида). Через точку на плоскости можно провести только одну прямую не пересекающую данную прямую.

История создания неевклидовой геометрии.

Через точку на плоскости можно провести только одну прямую не пересекающую данную прямую. Это единственная аксиома, которую постоянно пытались доказать.

Эти попытки занимали более 2-х тысячелетий до середины 19в. Тогда Н. И. Лобачевский доказал в своих трудах полную безнадежность этих попыток. 3 великих математика в 19в. Одновременно независимо друг от друга пришли к результату недоказанности 5 постулата и к созданию неевклидовой геометрии Лобачевского, Гаус, Байян.

История развития науки о числе.

2,5 тыс лет назад вавилоняне довольствовались лишь нат числами, подсчитывая кол-во овец. Сегодня ученые пользуются метрической алгеброй для описания 100 взаимосвязей. Числовые системы, применяем в математике могут быть расчленены на 5 гл ступеней

1) множество целых положительных чисел – натуральное множество N

2) относительные числа, включающие положительные числа, отрицательные числа и нуль;

3) рациональные числа, в которые входят целые числа и дроби;

4) – действительные

5) – комплексные числа

Особен матем стиля мышления.

А. Я. Хаичин раскрыл сущность стиля мат. мышления. Он выделил 4 общих для всех эпох черты заметно отличающие этот стиль от стиля мышления в др науках. Для математика характерно доведение до предела доминирования логической схемы рассуждения. Во-2 лаконизм,т.е сознают стремление находить кратчайший, ведущий к цели логический путь. В-3 четная расчлененность хода рассуждений.

В обыденном ненаучном мышлении часто наблюдается в таких случаях смешение и перескоки приводят к путанице и ошибкам в рассуждениях. В-4, скрупулезная точность формул и уравнений, т.е каждый мат символ имеет строго определенное значение.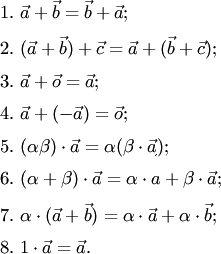

2 Билет

Определение комплексного числа

Комплекс число – число вида a+bi, где a и b– вещественная часть, i– мнимая часть

Свойства комплексных чисел

1) комплексные числа коммутативны по сложению и по умножению.

2) комплексные числа ассоциативны по сложению и по умножению.

3) комплексные числа дистрибутивны.

Операции над комплексными числами.

+

-

*

/

Модуль комплексного числа

Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ».

3 Билет

Понятие вектора

Вектор – направленный отрезок АВ с начальной точкой А и конечной В, который можно передвигать параллельно самому себе.

Основными понятиями аналитической геометрии являются простейшие геометрические образы (точки, прямые, векторы, плоскости, кривые).

Линейные операции над векторами

Сложение: Пусть a и b– 2 вектора. Вектор АС назыв суммой векторов а и в – правило трег-ка

параллелограмм диагональ AC – сумма векторов а и в

Вычитание: Разностью векторов а и в называется такой вектор, сумма которого с вектором b равна вектору а.

От некоторой точки А откладыв вектор АВ = вектору а. От этой же точки А отклад вектор АС =век в. Вектор СВ есть раз-ть векторов а и в.

Умнож-е вектора на число: Произв-ем ненулев вектора а на число k назыв такой вектор в, длина которого равна IkI*IaI причем векторы а и в сонаправл при k>=0 и противоположно направл при k<0.

Свойства линейных операций.

Сложение векторов коммутативно: .

Сложение векторов ассоциативно: .

Прибавление нулевого вектора к любому не меняет последнего: . Очевидно, .

Для любого вектора существует вектор такой, что или .

Умножение вектора на число ассоциативно: . Умножение вектора на число дистрибутивно относительно сложения чисел: .

Доказательство сводится к перечислению всех возможных знаков и , в каждом случае утверждение очевидно.

Умножение вектора на число дистрибутивно относительно сложения векторов: . Это следует из подобия треугольников и на рисунке.

Очевидно, умножение на единицу не меняет вектор: .

Скалярное произведение векторов.

Скал проив-ем векторов назыв произв-е их длин на cos угла между ними

4 Билет Уравнения прямой на плоскости.

y=kx+b x,y –коорд-ты точки, принадлеж этой прямой, k-угловой коээф-нт

Уравнение прямой проходящей через две точки.

Пусть даны точки A(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2) имеет вид:

Угол между прямыми на плоскости.

Угол α между двумя прямыми, заданными уравнениями: y=k1x+b1 (первая прямая) и y=k2x+b2 (вторая прямая), может быть вычислен по формуле: tg(α)=(k2-k1)/(1+k1k2)

Расстояние от точки до прямой.

Расстояние d от точки M1(x1;y1) до прямой Ax + By + C = 0 вычисляется по формуле:

D=(IAx₁+By₁+CI) / A²+B²

Кривые второго порядка.

Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению 2го порядка, где-a,b,c,d,f,g вещественные числа, и хотя бы одно из чисел отлично от нуля.

Общее уравнение кривой второго порядка.