28. Заменна переменной и интегрирование по частям в определенном интеграле

ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ  ИНТЕГРАЛЕ 

Предположим, что функция f (х) непрерывна на отрезке [a ; b],  функция   имеет на отрезке [ α ; β ] непрерывную  производную,  при этом  . Тогда   (2) Пример. Найти 

ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 

Пусть    — непрерывно  дифференцируемые на [a ; b]  функции.  Тогда справедлива формула         (3)  Пример. Найдем    . Положим    Согласно формуле (3) находим     = 

 

29 Геометрические приложения определенного интеграла.

ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР  

Пусть функция f (х)  непрерывна на отрезке [a ; b].  Если при этом f (х) ≥ 0 на [a ; b], то  площадь S криволинейной трапеции, ограниченной линиями  ,  выразится с помощью интеграла:     (1) 

Если же f (х) ≤ 0 на [a ; b], то −f (х) ≥ 0 на [a ; b].  Поэтому площадь S соответствующей  криволинейной трапеции находится по формуле    или     (2)  

Наконец, если линия у = f (х) пересекает ось Ох, то отрезок [a ; b] надо разбить на части, в  пределах которых f (х) не меняет знака, и к каждой части применить ту из формул (1) или (2),  которая ей соответствует.  

Пример 1. Найдем площадь плоской фигуры, ограниченной графиком функции у = sin х и осью  абсцисс при условии 0 ≤ х ≤ 2 π .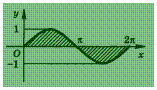   

Разобьем отрезок [ 0 ; 2π ] на два отрезка: [ 0 ; π ] и [ π ; 2π ].  На первом из них sin х ≥ 0, на втором sin х ≤ 0.  Тогда, используя формулы (1) и (2), находим искомую площадь:      Площадь криволинейного сектора ОАВ , 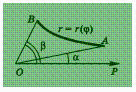 ограниченного лучами    и кривой АВ, заданной в полярной системе  координат уравнением  ,  где   — функция, непрерывная на отрезке [ α ; β ], выражается  формулой      (3)  Пример 2. Найдем площадь круга радиуса R.  В полярных координатах r, φ уравнение  окружности с центром в начале координат и радиусом R имеет вид 

, причем  .  Тогда, используя  формулу (3), получим   

30. Несобственные интегралы

При введении понятия определенного  интеграла мы предполагали, что подынтегральная функция является ограниченной, а пределы  интегрирования — конечными.  Такой интеграл называется собственным (слово  «собственный » обычно опускается).  Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.  

ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ  

Пусть функция f (х) непрерывна при   ,т. е. при х ≥ а.  Тогда по  определению полагают    Если этот предел существует, то говорят, что интеграл   сходится, а если предел не существует, то  интеграл называют расходящимся. Такому  интегралу не приписывают никакого значения.  

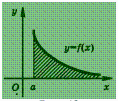
Геометрически для неотрицательной при х > а функции f (х) несобственный интеграл (1) по аналогии с собственным интегралом  представляет собой площадь фигуры, ограниченной  сверху графиком функции у = f (х), слева отрезком прямой х = а и снизу осью Ох :    Пример 1    т. е. данный несобственный интеграл сходится.  Пример 2    т. е. данный интеграл расходится.  Пример 3 Установим, при каких значениях α интеграл   сходится. Случай α = 1 был рассмотрен в примере 2.  Если α ≠ 1,то 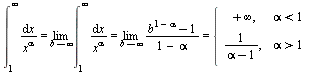   Значит, данный интеграл сходится при α > 1 и расходится при α < 1.  Все изложенное непосредственно переносится  на интеграл вида  ,  который  определяется так:    Наконец, по определению,  , где c — какое-нибудь число (выбор его  безразличен).  Последнее равенство следует понимать так: если каждый из интегралов, стоящих справа, сходится, то сходится и интеграл, стоящий слева. Если же расходится хотя бы один из интегралов, стоящих справа, то расходится и интеграл,  стоящий слева.  

31 Событие Алгебра событий

ПОНЯТИЕ О СЛУЧАЙНОМ СОБЫТИИ

Опыт, эксперимент, наблюдение явления называются испытаниями.

Примерами испытаний являются: бросание монеты, извлечение шара из урны, бросание игральной кости.

Результат, исход испытания называются событием.

Событиями являются: выпадение герба или цифры, взятие белого или черного шара, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используются заглавные буквы латинского алфавита: А, В, С и т. д.

Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.

Пример 1. Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В — появление четного числа очков. События А и B — совместимые.

Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Пример 2. Испытание: однократное бросание игральной кости. Пусть события A[1], A[2], A[3], A[4], A[5], A[6] — соответственно выпадение одного очка, двух, трех, четырех, пяти, шести. Эти события являются несовместимыми.

Два события А и conjugate(A) называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Пример 3. Испытание: бросание монеты. Событие А — выпадение герба, событие conjugate(A) — выпадение цифры.

Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.

Пример 4. Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное; событие В — вынут черный шар — невозможное.

Событие А называется случайным, если оно объективно может наступить или не наступить в данном испытании.

Пример 5. Событие A[6] — выпадение шести очков при бросании игральной кости — случайное. Оно может и не наступить в данном испытании.

АЛГЕБРА СОБЫТИЙ  

Суммой событий А и В называется событие С = А + В, состоящее в  наступлении по крайней мере одного из событий А или В.  Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадает в мишень первый стрелок, событие В —  попадает в мишень второй стрелок. Суммой событий А и В является событие С = А + В — попадает в мишень по крайней мере один стрелок.  Аналогично, суммой конечного числа  событий   называется событие  , состоящее в наступлении хотя бы одного из событий  .  

Из определения суммы событий  непосредственно следует, что  

А + В = В + А.  Справедливо также и сочетательное свойство. Однако  

А + А = А (а не 2А, как в алгебре).  Произведением событий А и В называется событие С = А В, состоящее в том, что в  результате испытания произошли и событие А, и  событие В.  Аналогично, произведением конечного  числа событий   называется событие   , состоящее в том, что в  результате испытания произошли все указанные  события.  В Примере 1 произведением событий А и В  является событие С = А В, состоящее в попадании в мишень двумя стрелками.  

Из определения произведения событий  непосредственно следует, что  

АВ = ВА.  

Справедливы также сочетательный и дистрибутивный законы. Однако  АA = А (а не   ).