18. Экстремум функции. Необходимые условия экстремума достаточные условия экстремума

Экстремум функции

Необходимое условие экстремума

      Функция g(x) в точке  имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки и для всех точек x  некоторой области:  , выполнено соответственно неравенство

(в случае максимума) или  (в случае минимума).

Экстремум функции находиться из условия: , если производная существует, т.е. приравниваем первую производную функции к нулю.

Достаточное условие экстремума

1) Первое достаточное условие: 

Если:

а) f(x) непрерывная функция и определена в некоторой окрестности точки  такой, что первая  производная в данной точке равна нулю или не существует.

б) f(x) имеет конечную производную в окрестности задания и непрерывности функции

в) производная сохраняет определенный знак справа от точки  и слева от этой же точки, тогда точку  можно охарактеризовать следующим образом

     Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.

2) Второе достаточное условие

     Если функция g(x) обладает второй производной  причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если  , то точка является максимумом; если  , то точка является минимумом.

3) Третье достаточное условие

     Пусть функция g(x) имеет в некоторой окрестности точки   N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:

а) Если N - четно, то точка   экстремум функции:  у функции точка максимума,    у функции точка минимума.

б) Если N - нечетно, то в точке  у функции g(x) экстремума не

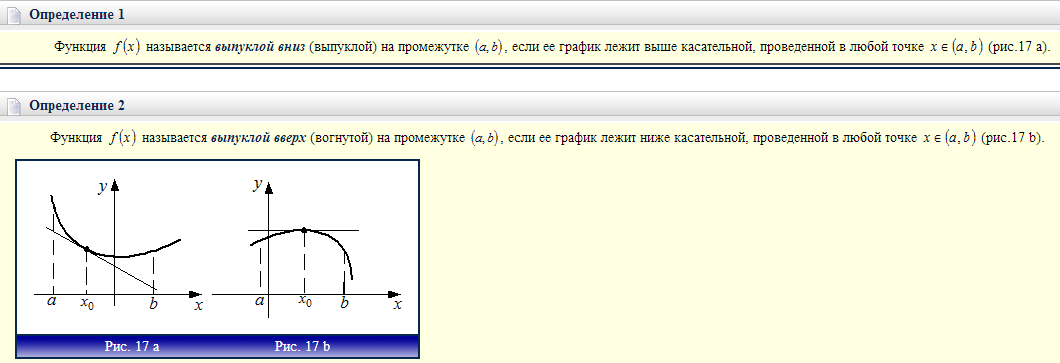
19. Выпуклость графика функции. Исследование с помощью второй производной. Точки перегиба.

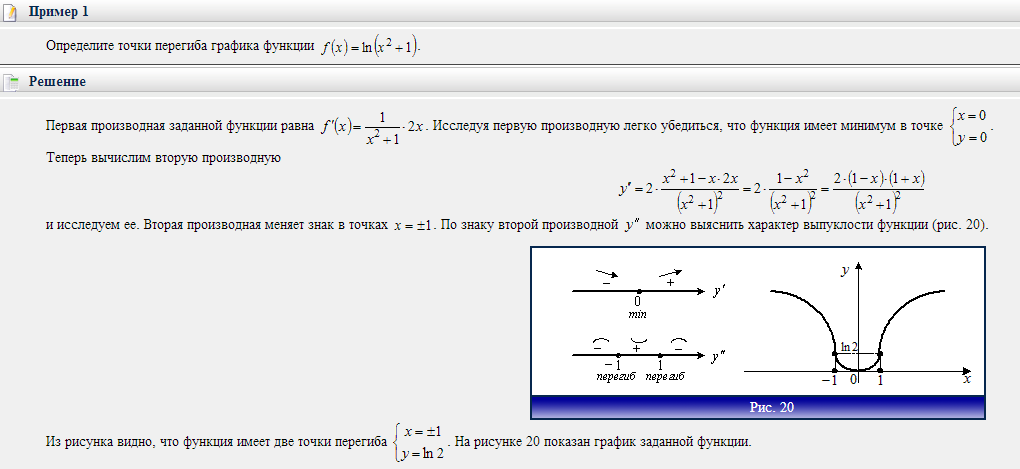
20. Асимптоты общая схема исследования функции.

Асимптоты графика функции

Определение 11 (вертикальная асимптота). Прямая x = a называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из пределов

lim_x® a+0f(x) или lim_x® a-0f(x)

равен +Ґ или -Ґ.

Пример 14. График функции y = 1/(x-2) имеет вертикальную асимптоту x = 2, так как lim_x® 2+01/(x-2) = +Ґ, lim_x® 2-01/(x-2) = -Ґ (рис.28).

Определение 12 (наклонная асимптота). Говорят, что прямая y = kx+b является наклонной асимптотой графика функции y = f(x) при x® +Ґ, если f(x) имеет вид

f(x) = kx+b+a (x),

где lim_{x® +Ґ}a (x) = 0.

Справедлива

Теорема 13 (существование асимптот). Для того чтобы график функции y = f(x) имел при x® +Ґ асимптоту y = kx+b, необходимо и достаточно, чтобы существовали два предела

lim_x® +Ґf(x)/x = k, lim_x® +Ґ(f(x)-kx) = b.

Доказательство.

1. Необходимость. Пусть график функции y = f(x) имеет при x® +Ґ асимптоту y = kx+b, то есть для f(x) имеет вид

f(x) = kx+b+a(x),

тогда

lim_x® +Ґf(x)/x = (kx+b+a(x))/x = k,

lim_x® +Ґ(f(x)-kx) = lim_x® +Ґ(b+a(x)) = b.

2. Достаточность. Пусть существуют пределы, фигурирующие в условии теоремы. Тогда величина f(x)-kx-b является бесконечно малой при x® +Ґ. Обозначив f(x)-kx-b = a(x) получим, что f(x) имеет асимптоту согласно определению наклонной асимптоты.

Замечание. Аналогично определяется наклонная асимптота и доказывается теорема 13 при x® -Ґ.

Замечание. Если k=0 в определении наклонной асимптоты, то наклонная асимптота является горизонтальной.

Пример 15. Найти асимптоты кривой:

y = 5x/(x-3).

Решение. Кривая имеет вертикальную асимптоту x = 3, так как

lim_x® 3± 05x/(x-3) = ±Ґ.

Найдем наклонную асимптоту:

k = lim_x® ±Ґy/x = lim_x® ±Ґ5x/x(x-3) = 0. b = lim_x® ±Ґ(y-kx) =lim_x® ±Ґ5x/(x-3) = 5.

Итак, данная кривая имеет вертикальную асимптоту x = 3 и горизонтальную асимптоту y = 5.

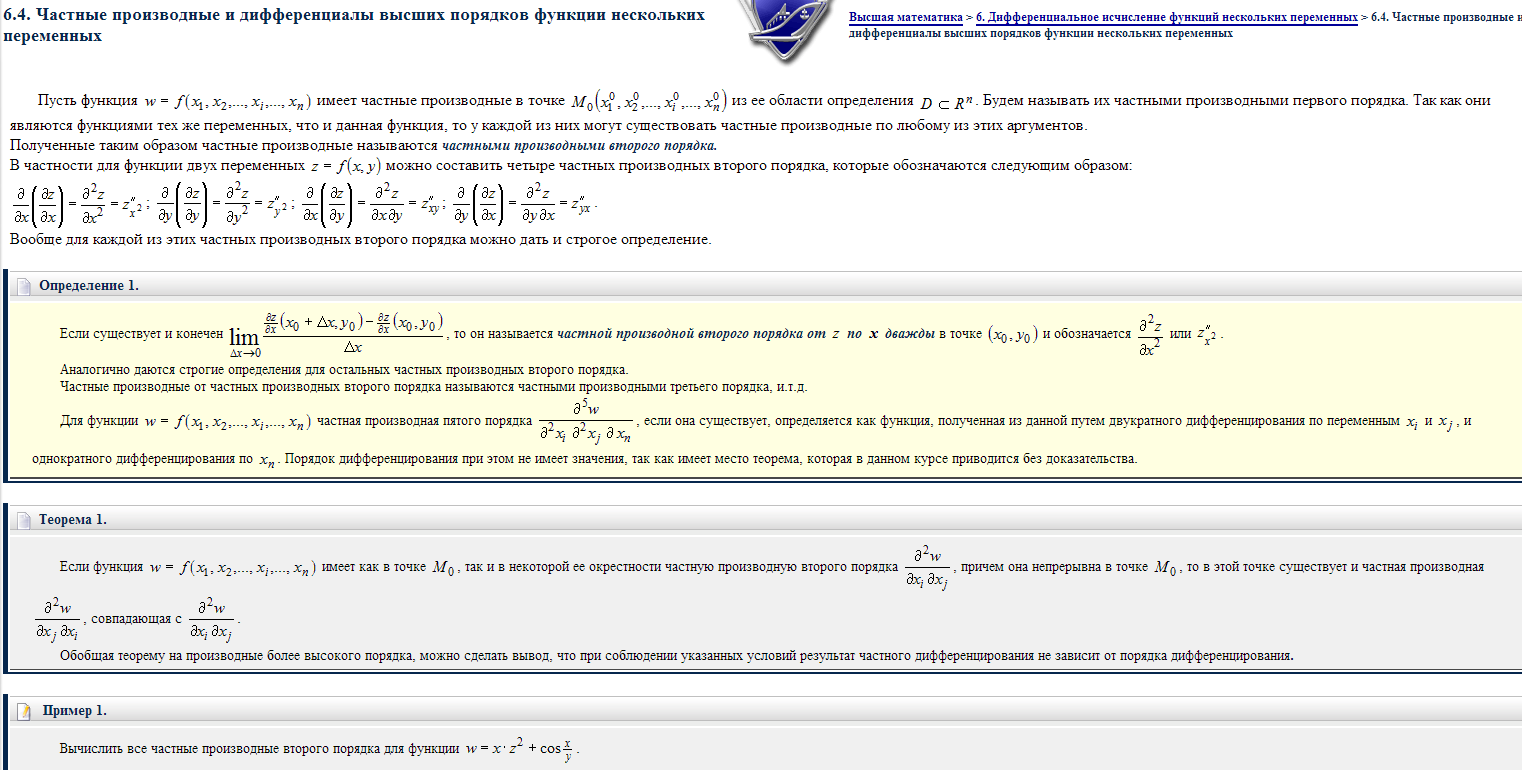
21. Частичные производные и дифференциал первого, второго порядка функции нескольких переменных.

22. Производная функция двух переменных по направлению. Градиент функции и его свойства

23.Экстримум функции двух переменных. Необходимое и достаточное условие локального экстримума функции двух переменных.

24. Условный экстремум. Наибольшее и наименьшее значение функции и замкнутой ограниченной области.

25. Первообразная. Понятие неопределенного интеграла. Свойства неопределенного интеграла.

Функция F (х) называется первообразной функцией для  данной функции f (х) (или, короче, первообразной данной функции f (х)) на данном промежутке, если на этом промежутке    . Пример. Функция    является  первообразной функции   на всей числовой оси, так как   при любом х.  Отметим, что вместе с  функцией   первообразной для   является любая функция вида  , где С —  произвольное постоянное число (это следует из того, что производная постоянной равна нулю). Это свойство имеет место и в общем случае.  

Теорема 1. Если   и   — две  первообразные для функции f (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.  Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной  функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С.  Выражение F (х) + С, где F (х) —  первообразная функции f (х) и С — произвольная  постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом  ,  причем f (х) называется подынтегральной функцией ;   — подынтегральным выражением,  х — переменной  интегрирования;  ∫ — знак неопределенного интеграла.  Таким образом, по определению    если  .  Возникает вопрос: для всякой ли функции f (х) существует первообразная, а значит, и  неопределенный интеграл?  Теорема 2. Если функция f (х) непрерывна на [a ; b], то на этом отрезке для функции f (х) существует первообразная.  Ниже мы будем говорить о первообразных лишь для непрерывных функций. Поэтому  рассматриваемые нами далее в этом параграфе  интегралы существуют. 

СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА

l. diff(int(f(x), x), x) = f(x)2. int(diff(F(x), x), x) = `+`(F(x), C)

3. Постоянный множитель можно вынести за знак интеграла: (1) 4. Интеграл от суммы двух функций равен сумме интегралов от этих функций:

int(`+`(f(x), g(x)), x) = `+`(int(f(x), x), int(g(x), x)) (2) Равенства (1) и (2) следует понимать с точностью до постоянного слагаемого.

Свойство 4 распространяется на случай алгебраической суммы любого конечного числа функций.

26.методы интегрирования

НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ 

Метод непосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путем преобразований и  применения свойств неопределенного интеграла.  Пример 1.    Пример 2. 

 

Пример 3.   

ЗАМЕНА ПЕРЕМЕННОЙ ИНТЕГРИРОВАНИЯ 

Этот способ часто бывает полезным в тех случаях, когда интеграл    (f (х) непрерывна) не может быть непосредственно преобразован к  виду табличного.  

Если   где   —  функция, имеющая непрерывную производную, то    .  Пример 1   

ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 

Пусть   и     — непрерывно дифференцируемые функции. Тогда справедлива формула   (4)   (4)  Пример 1  Найдем   

27. Определенный интеграл его геометрический смысл и свойства. Формула Ньютона – Лейбница.

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА  

Ниже рассматриваются функции, непрерывные на отрезке [a ; b].  

 

По определению полагают, что определенный интеграл от функции с равными верхним и нижним пределами интегрирования равен нулю:  . 1. Постоянный множитель можно выносить за знак определенного интеграла:  2. Определенный интеграл от суммы двух функций равен сумме определенных интегралов от этих функций:   

Это свойство распространяется на случай  алгебраической суммы любого конечного числа функций.  

3. При перестановке пределов  интегрирования определенный интеграл меняет знак на противоположный:   

4. Интеграл по отрезку равен сумме  интегралов по его частям:   

 

ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА  

Если функция f (х) непрерывна на отрезке  [a ; b] и F (х) — первообразная функции f (х) на этом отрезке, то   (1) Формула (1) называется формулой  Ньютона—Лейбница.  Пример 1    Пример 2