Вопрос 15

Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить стол­бец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 22 матрица планирования с учетом эффекта взаимодействия будет иметь вид

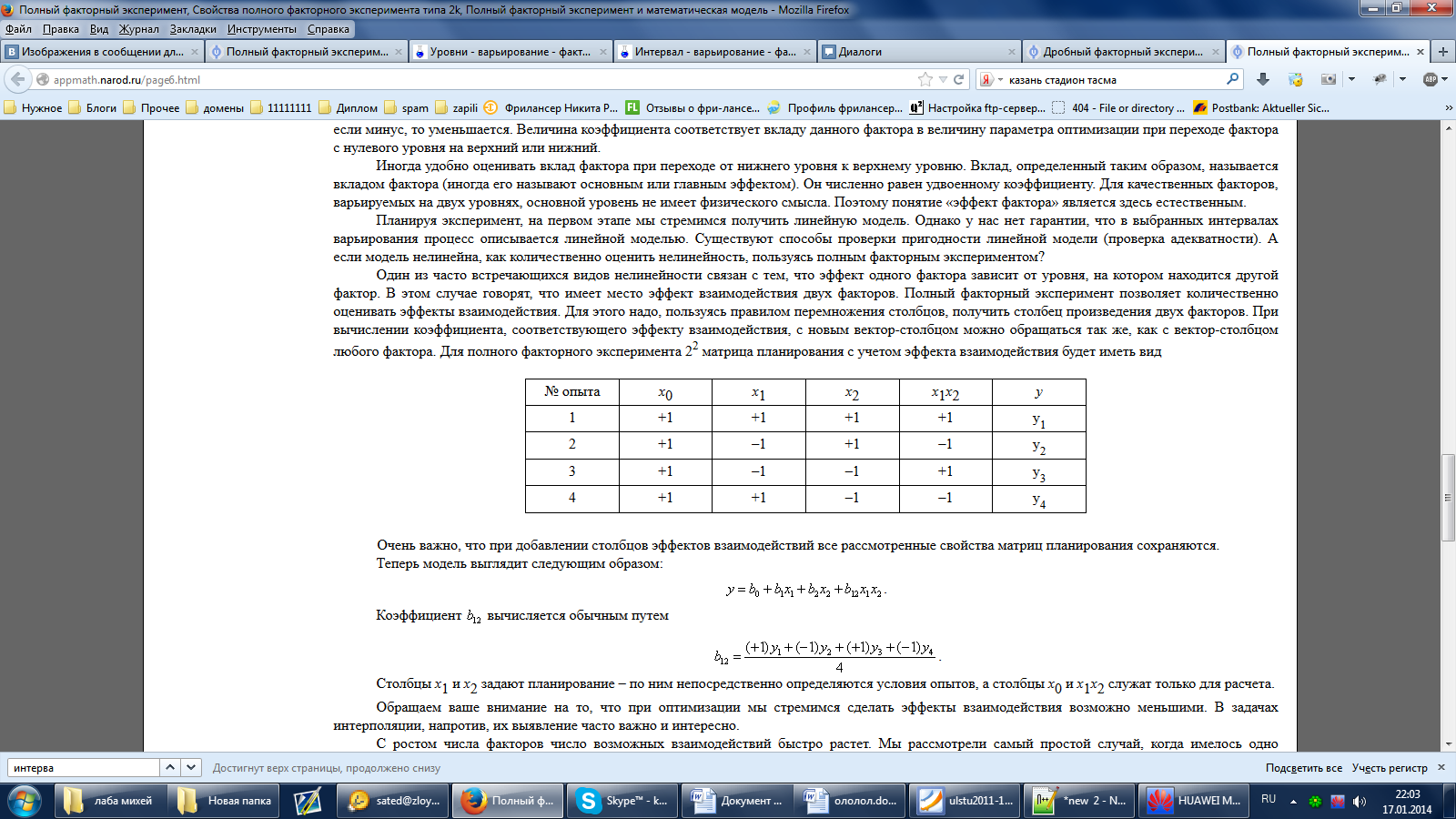
Столбцы x1 и x2 задают планирование – по ним непосредственно определяются условия опытов, а столбцы x0 и x1x2 служат только для расчета.

Обращаем ваше внимание на то, что при оптимизации мы стремимся сделать эффекты взаимодействия возможно меньшими. В задачах интерполяции, напротив, их выяв­ление часто важно и интересно.

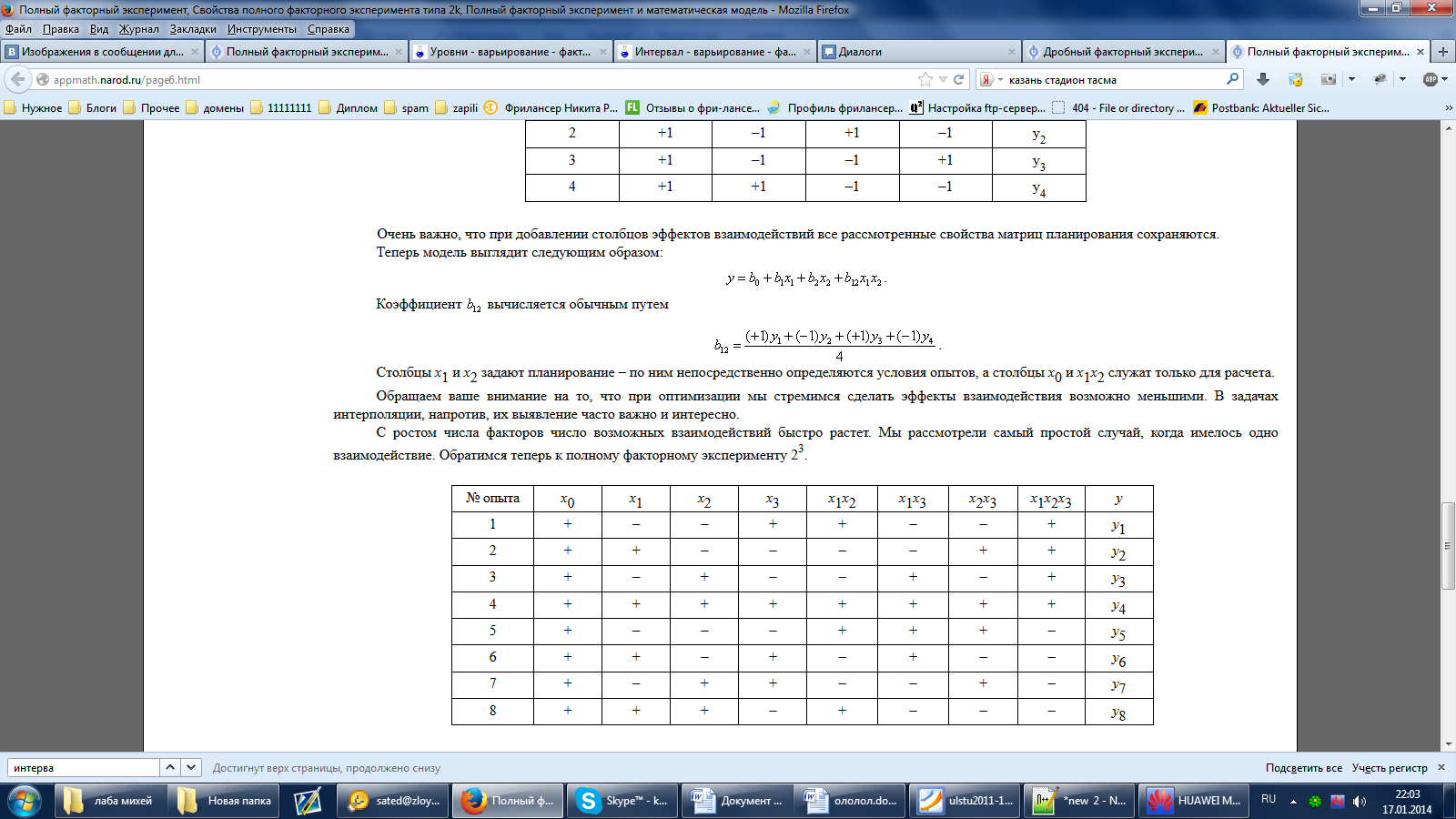
С ростом числа факторов число возможных взаимо­действий быстро растет. Мы рассмотрели самый простой случай, когда имелось одно взаимодействие. Обратимся теперь к полному факторному эксперименту 23.

Полное число всех возможных эффектов, включая b0, линейные эффекты и взаимодействия всех порядков, равно числу опытов полного факторного эксперимента. Чтобы найти число возможных взаимодействий некоторого по­рядка, можно воспользоваться обычной формулой числа сочетаний

Вопрос 16

Составление матрицы планирования ПФЭ

План ПФЭ изображают в виде таблицы, столбцы которой отражают уров-

ни факторов, а строки – номера опытов. Эти таблицы называют матрицами

планирования (МП) эксперимента. Поскольку значения уровней факторов по

модулю всегда равны единице, то обычно в МП записывают только знак уровня

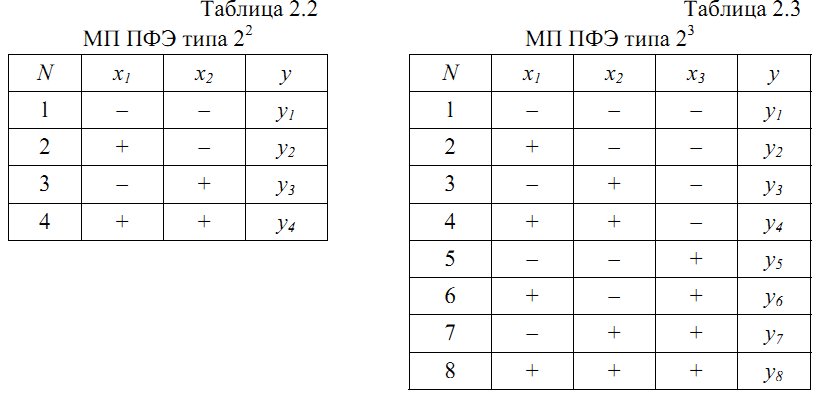
(т. е. «+» вместо «1» и «–» вместо «–1»). В табл. 2.2 для примера приведена МП

для ПФЭ типа 2², которую называют базовой, так как с ее помощью легко построить матрицы любого порядка.

Так, для построения матрицы 2³ сочетаем базовую матрицу с нижним и

верхним уровнями x3 (табл. 2.3). Легко заметить, что в первом столбце знаки

меняются поочередно, во втором через 2, в третьем через 4 и так далее.

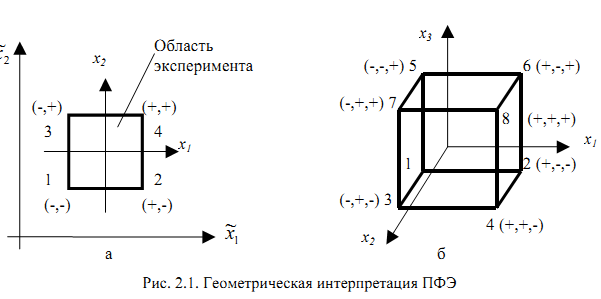
Геометрической интерпретацией ПФЭ 22 является квадрат в факторной плоскости (рис. 2.1, а), ПФЭ 23 – куб (рис. 2.1, б).

Здесь нормированные координаты x1 и x2 проходят через точку пересече-

ния основных уровней факторов, и масштаб их осей выбран так, чтобы интер-

вал варьирования равнялся 1. Тогда условия проведения опытов в МП экспери-

мента будут соответствовать вершинами квадрата, центром которого является

основной уровень. Если n>3, то фигуру, задающую в многомерном пространст-

ве область эксперимента, называют гиперкубом.

Влияние факторов на выходной параметр может зависеть от уровня, на ко-

тором находится другой фактор, или от сочетания уровней нескольких факто-

ров. Если априорно не известно, что такой зависимости между факторами нет,

то строят развернутую МП, учитывающую не только факторы, но и их взаимо-

действия. При этом знаки в столбцах для взаимодействий получают перемно-

жением знаков взаимодействующих факторов. Пример развернутой МП для

ПФЭ дан в табл. 2.4.

Фиктивный фактор x0 вводят для удобства машинного расчета свободного

члена b0 (для идентичности формул).

Основные свойства МП эксперимента:

а) симметричность относительно центра эксперимента

Свойство ортогональности позволяет упростить вычисления и получить

независимые оценки коэффициентов регрессии. Это означает, в частности, что

замена нулем любого коэффициента в уравнении ММ не изменит оценок ос-

тальных коэффициентов. Это свойство может быть полезным, когда точный вид

модели не известен и требуется по экспериментальным данным отобрать фак-

торы, существенно влияющие на исследуемый параметр. Если условие ортого-

нальности не выполняется, после исключения каждого незначимого коэффици-

ента необходимо пересчитывать оценки оставшихся коэффициентов и их дис-

персии. При этом могут измениться как доверительные интервалы, так и выво-

ды относительно коэффициентов значимости;

г) рототабельность – свойство равноточного предсказания исследуемого

параметра на равных расстояниях от центра эксперимента вне зависимости от

направления. Матрица, удовлетворяющая условиям симметричности, нормировки и ортогональности, называется оптимальной. МП ПФЭ является оптимальной для линейных ММ. Если же ММ содержит взаимодействия, то свойство рототабельности не выполняется.