Вопрос 13 - 14

Полный факторный эксперимент (ПФЭ) – совокупность нескольких измерений, удовлетворяющих следующим условиям:

Количество измерений составляет 2n, где n – количество факторов;

Каждый фактор принимает только два значения – верхнее и нижнее;

В процессе измерения верхние и нижние значения факторов комбинируются во всех возможных сочетаниях.

Преимуществами полного факторного эксперимента являются

простота решения системы уравнений оценивания параметров;

статистическая избыточность количества измерений, которая уменьшает влияние погрешностей отдельных измерений на оценку параметров.

Целью планирования эксперимента, как правило, является получение математической модели (ММ) исследуемого объекта или процесса. Если на объект

действует много факторов, механизм которых неизвестен, то обычно используют полиномиальные ММ (алгебраические полиномы), называемые уравнениями

регрессии. Так, для двух факторов x1 и x2:

полином 0-й степени: y = b0;

полином 1-й степени: y = b0 + b1x1 + b2x2 – линейная модель;

полином 2-й степени: y = b0 + b1x1 + b2x2 + b12x1x2 + b11x12+ b22x22 – полная квадратичная модель.

При планировании эксперимента исследуемый объект представляется

«черным ящиком» (рис. 1.1), на который воздействуют факторы xi.

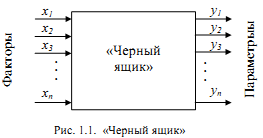
Каждый фактор xi может принимать определенное количество значений,

называемых уровнями факторов. Множество возможных уровней фактора xi

называется областью его определения. Эти области могут быть непрерывными

и дискретными, ограниченными и неограниченными. Как уже отмечалось,

должна быть возможность управления факторами: либо поддерживать их на за-

данном уровне, либо изменять по программе.

Факторы должны быть совместимыми и независимыми. Совместимость

предполагает допустимость любой комбинации факторов, а независимость –

отсутствие между факторами корреляционной связи.

К исследуемым параметрам также предъявляют ряд требований.

Они должны быть:

- эффективными, то есть способствовать скорейшему достижению цели;

- универсальными – быть характерными не только для исследуемого объекта;

- статистически однородными, то есть определенному набору значений

факторов xi с точностью до погрешности эксперимента должно соответствовать определенное значение фактора yi;

- выражаться количественно одним числом;

- легко вычисляться и иметь физический смысл;

- существовать при любом состоянии объекта.

Геометрический аналог параметра (функции отклика) называется поверх-

ностю отклика, а пространство, в котором строят эту поверхность, – фактор-

ным пространством. Размерность факторного пространства равна числу фак-

торов. Так, например, при двух факторах факторное пространство представляет

собой факторную плоскость.

При планировании эксперимента требуемых свойств ММ добиваются вы-

бирая условия проведения опытов. Множество точек факторного пространства,

в которых проводится эксперимент, представляется с помощью плана экспери-

мента

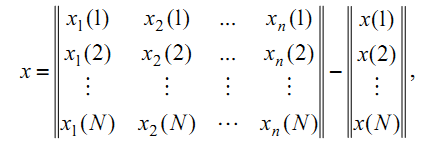
где n – число факторов; N – число точек факторного пространства. Точка

, называется центром плана. Если центр плана совпадает с на-

чалом координат, то план называется центральным.

Условия проведения опытов могут свободно выбираться в пределах задан-

ных границ. Выбор соответствующего плана эксперимента позволяет обеспе-

чить ММ разные свойства. Наиболее распространенными являются следующие

критерии.

Критерий ортогональности – когда полученные оценки коэффициентов

регрессии некоррелированы (не смешаны). Замена нулем любого коэффициента

в ММ в этом случае не изменяет значений остальных коэффициентов.

Критерий рототабельности – когда дисперсия выходной переменной зави-

сит только от расстояния от центра плана.

Критерий A-оптимальности требует выбора такого плана, при котором

дисперсионная матрица имеет минимальный след (минимальную сумму диаго-

нальных элементов).

Критерий D-оптимальности требует минимизации определителя дисперси-

онной матрицы.

Критерий G-оптимальности требует достижение наименьшей величины

максимальной дисперсии зависимой переменной.