15(1). Оценивание параметров распределений.

Статистические параметры обычно оцениваются по выборкам. Т.о. выборка будет хорошо отображать репрезентативность (представительность) генеральной выборки (совокупности).

В промышленности могут оцениваться партии выпущенной продукции (либо серии из партии). Отобранные продукции исследуют и получают случайную величину.

Xи=Xд + E

E- нормально распределенная случайная величина.

Xд – детерминированная величина.

Плотность НР:

Считается, что процесс контролируемый, если контролируется дисперсия (можно влиять).

Почему нормальное распределение?

Величина E зависит от множества причин, которые вносят одинаковый вклад, т.е. ни одна причина не доминирует. В этом случае мы находимся в условиях теоремы Липунова.

E=Σni; ni – случайное отклонение, вызванное i-ой причиной.

Отклонение д.б. в разные стороны от детерминированной величины.

Сумма Σni сводится к нормальной величине, если i=5-7; т.е. когда существует 5-7 причин.

Нормальное распределение случайной величины (псевдослучайной величины) можно получить с помощью функции Random.

Случайное событие – это псевдослучайное событие в котором заложен линейный процесс. Случайность достигается за счет колебаний, округлений; связанных с динамическим хаосом (нелинейность + неустойчивость).

15(2).

16(1). Свойства распределений. Биномиальное, нормальное.

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

P { a-3δ ≤ ξ ≤ a+3δ } = 0,9973 (правило 3-х сигм)

Xmax-Xmin = a-3δ - a+3δ = 6δ

- выполняется с вероятностью p=0.9973

У каждой статистической оценки есть характеристики:

1. Точность.

2. Достоверность (надежность, доверительная вероятность).

Точность обратно пропорциональна достоверности, т.е. при увеличении точности – достоверность падает, и наоборот.

Свойства:

Если случайные величины X₁ и X₂ независимы и имеют нормальное распределение с математическими ожиданиями μ₁ и μ₂ и

16(2).

дисперсиями и соответственно, то X₁ + X₂ также имеет нормальное распределение с математическим ожиданием μ₁ + μ₂ и дисперсией .

Биномиа́льное распределе́ние — это распределение числа заданных случаев в последовательности из «n» испытаний каждый из которых происходит с вероятностью «p», и не происходит с вероятностью «q».

Свойства биномиального распределения

• Пусть Y₁∼Bin(n,p) и . Тогда .

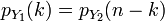• Пусть Y₁∼Bin(n₁,p) и Y₂∼Bin(n₂,p). Тогда Y₁ + Y₂∼Bin(n₁ + n₂,p).

Связь с другими распределениями

• Если , то получаем распределение Бернулли.

• Если большое, то в силу центральной предельной теоремы , где  — нормальное распределение с математическим ожиданием 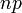и дисперсией .

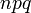• Если большое, а  — фиксированное число, то , где  — распределение Пуассона с параметром .

17(1). Критерии согласия: – χ² квадрат, критерий Колмогорова.

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу о том, что эта случайная величина подчиняется закону распределения . Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение исследуемой случайной величины. Сравнение эмпирического распределения и теоретического (или, точнее было бы сказать, гипотетического — то есть соответствующего гипотезе ) распределения производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Статистика критерия

Для проверки критерия вводится статистика:

где  — предполагаемая вероятность попадания в -й интервал,  — соответствующее эмпирическое значение,  — число элементов выборки из -го интервала,  — полный объём выборки. Также используется расчет критерия по частоте, тогда:

где  — частота попадания значений в интервал. Эта величина, в свою очередь, является случайной (в силу случайности ) и должна подчиняться распределению .

Правило критерия Если полученная статистика превосходит квантиль закона распределения заданного уровня значимости с или с степенями свободы, где — число наблюдений или

17(2).

число интервалов (для случая интервального вариационного ряда), а — число оцениваемых параметров закона распределения, то гипотеза отвергается. В противном случае гипотеза принимается на заданном уровне значимости .

На практике кроме критерия часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения

,

называемой статистикой критерия Колмогорова.

Доказано, что какова бы ни была функция распределения непрерывной случайной величины , при неограниченном увеличении числа наблюдений вероятность неравенства стремится к пределу

.

Задавая уровень значимости , из соотношения

можно найти соответствующее критическое значение .

Схема применения критерия Колмогорова следующая:

1. Строятся эмпирическая функция распределения и предполагаемая теоретическая функция распределения .

2. Определяется мера расхождения между теоретическим и эмпирическим распределением по формуле (1) и вычисляется величина .

3. Если вычисленное значение окажется больше критического _, определенного на уровне значимости , то нулевая гипотеза о том, что случайная величина имеет заданный закон распределения, отвергается (односторонний критерий). Если , то считают, что гипотеза не противоречит опытным данным.