10(1). Когнитивная структуризация. Когнитивные карты

З наковый ориентированный граф:

-прямая пропорциональная зависимость

-обратная пропорциональная зависимость

Пример:

	Численность	Рождения	Уровень загр.	Потребление кислорода
Численность	0	1	1	-1
Рождения	1	0	0	0
Уровень загр.	-1	-1	0	0
Потребление кислорода	1	1	0	0

Матрица смежности: [P]=

10(2).

«1» - если «+» на связи,

«0», если нет связи,

«-1» - если «-» на связи.

Начальный импульс был (1000), умножим этот импульс на эту матрицу, получим (011-1)

11(1). Эргодические цепи Маркова и их приложения.

Время дискретно, число состояний конечно, переходы осуществляются случайным способом, мгновенно. Время измеряется номером очередного шага.

Состояние системы в следующий момент времени (на след шаге) зависит только от состояния системы в данный момент и не зависит от предыстории (т.е. от того, каким способом система пришла в данное состояние).

Цепью Маркова называется случайная последовательность натуральных чисел, удовлетворяющему Марковскому свойству.

- матрица переходов

11(2).

Свойство матриц переходов:

- характерное свойство для переходных матриц (стохастическая матрица). При возведении в большую степень матрица вырождается.

Независимо от начального состояния установится стационарное состояние, т.е. статистическое равновесие. Если

n-ое состояние стационарно, то после следующего шага оно не изменится.

Эргодическая теорема для конечных однородных цепей Маркова, т.е. равновесный вектор, представляет собой левый неподвижный вектор.

12(1). Балансные модели. Модель Леонтьева.

Балансовые модели, как статистические, так и динамические, широко применяются при экономико-математическом моделировании экономических систем и процессов. В основе создания этих моделей лежит балансовый метод, т.е. метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Если описывать экономическую систему в целом, то под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребностью в этой продукции. При таком подходе рассматриваемая система состоит из экономических объектов, каждый из которых выпускает некоторый продукт, часть его потребляется другими объектами системы, а другая часть выводится за пределы системы в качестве ее конечного продукта. Если вместо понятия продукт ввести более общее понятие ресурс, то под балансовой моделью следует понимать систему уравнений, которые удовлетворяют требованиям соответствия наличия ресурса и его использования. Кроме приведенного выше требования соответствия производства каждого продукта и потребности в нем, можно указать такие примеры балансового соответствия, как соответствие наличия рабочей силы и количества рабочих мест, платежеспособного спроса населения и предложения товаров и услуг и т. д. Важнейшие виды балансовых моделей: • частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей;• межотраслевые балансы; • матричные техпромфинпланы предприятий и фирм. Балансная модель Леонтьева

Вся экономическая модель является замкнутой. Несколько секторов экономики обмениваются товарами. Балансная модель Леонтьева – является мультикомпартментной.

12(2). X=Ax+C (x и C - вектора) – уравнение стоимостного баланса.

С – является стимулом экономического производства.

Формула Ньютона-Лейбница.

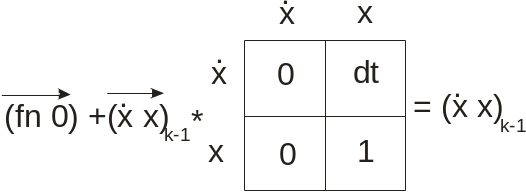
Р ешаем: