- •1(1). Методы системного анализа и теории управления в исследовании хозяйственной деятельности
- •2(1). Основные свойства систем и их элементов.
- •3(1). Исследование систем методом моделирования.
- •4(1).Событийный подход к моделированию. Причинно-следственные отношения и закономерности.
- •5(1). Математическое представление причинно – следственных связей.
- •6(1). Принцип эквивалентности Беллмана и вероятностная причинность.
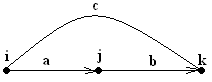
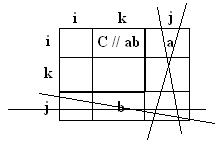
- •7(1). Сигнальные графы: основные свойства и элементарные преобразования
- •8(1). Формула Мэзона и её приложения.
- •9(1).Марковские процессы с ресурсными оценками. Алгоритм Байцера.
- •10(1). Когнитивная структуризация. Когнитивные карты
- •11(1). Эргодические цепи Маркова и их приложения.
- •12(1). Балансные модели. Модель Леонтьева.
- •13(1). Статистические методы исследования больших систем
- •14(1). Идентификация систем. Модель «черного ящика».
- •15(1). Оценивание параметров распределений.
- •16(1). Свойства распределений. Биномиальное, нормальное.
- •18 (1). Некоторые положения теории случайных процессов. Корреляция.
- •19. 20.(1) Установление зависимостей. Линейная регрессия. Квадратическая регрессия (теория для регрессии общая).
- •21 (1). Модели теории массового обслуживания. Основные положения.
- •22 (1). Правило составления уравнений Колмогорова
- •23(1). Интерполирование зависимостей. Фундаментальный полином Лагранжа.
- •24 (1). Статистический контроль качества, общие положения.
- •25(1). Изменчивость и воспроизводимость технологических процессов.
- •26 (1). Этапы организации контроля качества.
- •27(1). Контрольные карты (кк)
- •28(1). Критерии полезности при оценке качества систем. Максимизация полезности
- •29(1). Качество и надежность систем хозяйственной деятельности.
- •30 (1). Методы и модели теории надёжности.
- •31(1). Надёжность систем управления: комплексы технических средств.
- •32 (1) . Надёжность человека–оператора, менеджера, лпр.
- •33(1). Соотношение надежности и стоимости. Показатели надёжности систем.
- •34(1). Надёжность компьютерных систем и технологий. Общие положения.
- •35(1). Структура информационных технологий управления производственным процессом.
- •36 (1). Программное обеспечение и его надежность.
- •37(1). Структура процесса принятия решений. Проблемная ситуация.
- •38(1). Внешняя и внутренняя среда системы как факторы управления.
- •39 (1). Функции управления по Павлову.
- •40(1). Полный алгоритм достижения целей по Павлову.
- •41(1). Планирование в процессе управления предприятием.
- •42(1). Принципы планирования хозяйственной деятельности.
- •Принцип своевременности.
- •Принцип участия каждого руководителя в процессе планирования.
- •Принцип преемственности плана.
- •43(1). Критерии эффективности систем деятельности.
- •44(1). Деловые игры, основные аспекты.
- •45(1). Этапы проведения деловых игр.
- •46(1). Документирование результатов деловой игры.
- •47(1). Инновационная деятельность в организациях, общие понятия.
- •48(1). Методы поиска новых идей: метод мозгового штурма
- •49(1). Метод Синектики.
- •50(1). Теория решения изобретательских задач Альтшуллера
8(1). Формула Мэзона и её приложения.
Общая формула от одной входной вершины (исток) к выходной (сток) (для сигнальных графов) (топологическая формула Мэзона).
![]()
![]() -
веса
-
веса
![]() -
определитель графа
-
определитель графа
Сумма передач всех прямых путей от истока к стоку, умноженную на веса этих путей, деленное на определитель графов.
![]() GiGj
– те контура которые не касаются друг
друга
GiGj
– те контура которые не касаются друг
друга
![]()
Иначе,
![]() который
может быть получен из исходного графа
после исключения исходного прямого
пути вместе с ребрами, которые касаются
этого пути.
который
может быть получен из исходного графа
после исключения исходного прямого
пути вместе с ребрами, которые касаются
этого пути.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8(2).

Применение формулы Мэзона для решения СЛАУ.

![]()
По b1 и b2 найти х1и х2 . Т.е. х1и х2сделать следствиями.


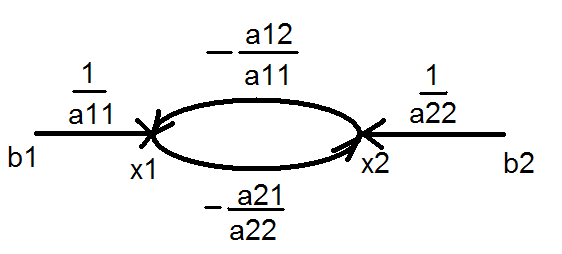
И далее по формуле Мэзона.
9(1).Марковские процессы с ресурсными оценками. Алгоритм Байцера.
Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временного параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»).

Диаграмма переходов в скрытой марковской модели (пример) x — скрытые состояния y — наблюдаемые результаты a — вероятности переходов b — вероятность результата
Структура скрытой марковской модели
В обычной Марковской модели состояние видимо наблюдателю, поэтому вероятности переходов — единственный параметр. В скрытой Марковской модели мы можем следить лишь за переменными, на которые оказывает влияние данное состояние.
Из диаграммы становится ясно, что значение скрытой переменной x(t) (в момент времени t) зависит только от значения скрытой переменной x(t − 1) (в момент t − 1). Это называется свойством Маркова.

Вероятность увидеть последовательность Y=y(0),y(1),…y(L-1)
длины L равна
P(Y)=
![]() P(Y|X)P(X),
здесь сумма пробегает по всем возможным
последовательностям скрытых узлов
Х=х(0),х(1)...x(L-1). Метод
подсчёта полным перебором значений P(Y) —очень
трудоёмкий для многих задач из реальной
жизни в силу того, что количество
P(Y|X)P(X),
здесь сумма пробегает по всем возможным
последовательностям скрытых узлов
Х=х(0),х(1)...x(L-1). Метод
подсчёта полным перебором значений P(Y) —очень
трудоёмкий для многих задач из реальной
жизни в силу того, что количество
9(2). возможных последовательностей скрытых узлов очень велико. Но применение процедуры вперёд-назад позволяет существенно увеличить скорость вычислений.
Алгоритм Байцера.



Могут появится неприятности в виде появления пятен:
![]() по
формуле
по
формуле