6(1). Принцип эквивалентности Беллмана и вероятностная причинность.
Принцип Беллмана:
Если события связаны в цепочку как Причина и Следствие, то они образуют цепь Маркова.
Далее нужно составить матрицу смежности (переходы из вершин в вершину).
Сигнальный граф – представляет собой ориентированный граф.
1). Материальная основа.
2). Структура.
Причина не транзитивна.
A->B; B->C. Это не значит, что A->C.
В статистической механике состояние системы характеризуется не набором точных значений координат и импульсов всех частиц, а функцией распределения, определяющей вероятность того, что координаты и импульсы частиц системы имеют определенные значения, т. е. то, как часто в ансамбле тождественных систем встречаются различные распределения значений координат и импульсов частиц. По функции распределения в данный момент времени (при известной энергии взаимодействия) можно однозначно найти вероятность появления определенных значений координат и импульсов частиц в любой последующий момент времени; они рассматриваются как случайные величины, не определяемые однозначно макроскопическими условиями (температурой, давлением, объёмом и т. д.), в которых находится система.
6(2).
Таким образом, в этом случае причинно связаны вероятности координат и импульсов.
Это новая форма Причинности - вероятностная причинность, понимание которой в основном остаётся прежним: состояние системы в данный момент однозначно определяется состоянием системы в предшествующий момент, однако способ описания состояния становится новым, вероятностным.
7(1). Сигнальные графы: основные свойства и элементарные преобразования
Сигнальный граф – это ориентированный граф, соответствующий линейным или линеаризированным системам уравнений математической модели технической системы и отражающий причинно-следственные связи между переменными (сигналами) системы. Вершины сигнального графа соответствуют сигналам, а ветви – коэффициентам или передаточным функциям, характеризующим связь между этими сигналами. Таким образом, каждая ветвь сигнального графа отображает причинно-следственную связь между сигналами (переменными), образующими начало и конец ветви, причём начало ветви истолковывается как причина, а её конец как следствие. Направление ветви указывает от причины к следствию. Вершины-источники сигнального графа отображают независимые (свободные) переменные, вершины-стоки – зависимые переменные технических систем. Вершины, соответствующие входящим и исходящим ветвям, называют смешанными. Их относят к зависимым переменным и называют зависимыми вершинами.
Построение сигнальных графов выполняют на основании следующих правил:
1.Сигналы передаются вдоль ветвей только в направлении их ориентации.
2.Сигнал, проходящий вдоль какой-либо ветви, умножается на передачу этой ветви.
3.Сигнал, изображаемый какой – либо вершиной, является суммой всех сигналов, только приходящих в эту вершину (узел).
4.Значение сигнала, изображаемого какой-либо вершиной, передаётся по всем ветвям, выходящим из неё.
Согласно этих правил значение сигнала в любой зависимой вершине сигнального графа определяется формулой.
,
где
–
значение сигнала в k - ой вершине
сигнального графа; j=1, N – число вершин
графа, связанных выходящими ветвями с
k -м узлoм;
-
коэффициент передачи ветви, входящих
в k - ю вершину.
a,b,c – коэффициенты передачи. Если ищем конечный результат или первоначал причину ab….c x ----- t
При последовательном соединении коэффициенты передачи перемножаются. При параллельном – складываются.
7(2). Прямым путем – из вершины i в вершину j называется последовательность вершин и дуг, идущих вдоль стрелок и не проходящие дважды одну и туже вершину. Передача прямого пути равна произведению передач дуг, входящих в этот прямой путь. Контур – замкнутый прямой путь. Передача контура - произведение передач дуг входящих в этот контур. Теория сигнальных графов и теория СЛАУ изоморфны. Контура касаются друг друга, если у них есть хотя бы одна общая вершина. Аналогично, прямые пути и контура касаются друг друга, если у них есть хотя бы одна общая вершина.
Преобразование сигнальных графов.
а)
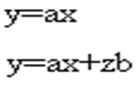
б)
в)
г)
