27(1). Контрольные карты (кк)

Появились в 1924 г. в США (Шухарт)

Назначение карт:

1) Определение требуемого уровня (номинала) процесса, на достижение которого должен быть нацелен персонал;

2) Используются как вспомогательные средства для достижения номинала;

3) Служат в качестве основы для определения отклонения от номинала или соответствия ему.

КК представляют собой временной график выборочных характеристик и w_i при контроле по количественному признаку и число _____ по качественному признаку.

На КК наносятся границы, показывающие моменты разладки процесса. Соответственно, по КК принимается решение о прекращении производства; наладке оборудования и т.п.

в Англии:

Предупреждающая граница: уровень значимости = 0,025;

Граница регулирования: УЗ = 0,001.

в США:

одна граница: УЗ = 0,027

S(x)=	S
	 n

– можно наносить на КК средние значения

– предупреждающая граница;

– граница регулирования (принятие решения)

Для дискретного (качественного признака):

D_x = npq; q = 1 – p

– для биномиального распределения

Каждое решение имеет риск. Минимакс – безрисковый критерий.

Риск:

R = Q  P_Q

Q ­­– объем потерь

P_Q – вероятность потерь

27(2).

28(1). Критерии полезности при оценке качества систем. Максимизация полезности

Полезность - функция, выражающая предпочтение потребителя при выборе товаров. Потребитель может выразить предпочтения в форме: х1>х2; х1<х2; х1 эквивалентно х2. Считается, что на рынке потребителю предлагаются наборы благ, цены этих благ диктуются рынком. Потребитель обладает правом свободного выбора. У потребителя имеется ограниченный запас средств или денег. Блага имеют обычные измерители (физические и стоимостные). К благам относится все, что служит удовлетворению потребностей, а так же иной труд, который является источником всех остальных благ. Цены постоянны и диктуются рынком. Модели теории предельной полезности и производственной функции основана на аксиоматике.

Аксиоматика:

• Аксиома сравнимости: для любых 2-х наборов благ xi, xj потребитель может сформировать 3 высказывания:

1. x_i > x_j, x_i предпочтительнее x_j

2. x_i < x_j

3. x_i ~ x_j

Существуют физические измерители стоимости | x_i || x_j | и известно что:

| x_i | > | x_j | => x_i > x_j

| x_i | > | x_j | => x_i < x_j

| x_i | = | x_j | => x_i ~ x_j

• Аксиома насыщенности спроса.

• Аксиома треугольника или вогнутости: существует функция полезности U(xi) и U(xj) и число

• 0≤ α ≤ 1, тогда

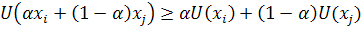
Ф ункция полезности смеси выпукла или вогнута. Смеси предпочтительнее, т.к. это снижает риск.

28(2).

Аксиома ограниченности бюджета: существует наборы {xi}, вектор цен {Рi}, тогда скалярное произведение меньше бюджета , где М – величина бюджета.

Для того чтобы максимизировать полезность при заданном фиксируемом количестве расходуемых денег, индивид будет покупать такие количества товаров, которые полностью исчерпывают его доход и для которых норма замещения (MRS) равна норме обмена между двумя этими товарами на рынке (обратному соотношению цен этих товаров):

Предположим, что отношение предпочтения обладает свойствами сравнимости, транзитивности, рефлексивности, непрерывности, строгой монотонности и строгой выпуклости. Представляющая это отношение предпочтения функция полезности является непрерывной, возрастающей, строго квази-вогнутой и дифференцируемой во всех точках. Потребитель может потреблять только неотрицательные количества каждого блага:

Пусть бюджетное множество является ограниченным, замкнутым, непустым и выпуклым. Допустим, что наша задача имеет решение в виде «внутреннего» максимума, при котором потребитель покупает ненулевые количества всех благ из товарного набора, то есть xi > 0 ∀i .

Л егко видеть, что мы имеем дело с задачей на условный экстремум, которую можно решить, используя метод множителей Лагранжа. Выпишем функцию Лагранжа для данной задачи:

28(3).

Необходимым условием (или условием первого порядка) максимума функции является равенство нулю всех её частных производных:

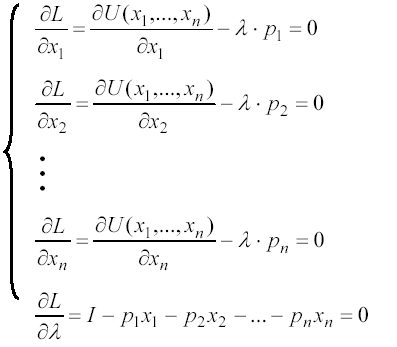
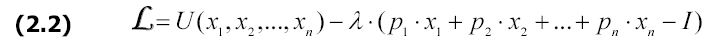
Решив эту систему уравнений, мы найдём значения x1 , x2 ,..., xn , которые являются оптимальными количествами каждого из благ, то есть такими количествами, которые максимизируют полезность индивида от потребления данного товарного набора при заданном бюджетном ограничении. Именно на эти количества каждого блага наш потребитель предъявит спрос на рынке.

Разумеется, условие первого порядка является лишь необходимым, но не достаточным условием максимума функции. Мы значительно облегчим задачу, введя предпосылку о строгой выпуклости отношения предпочтения. Если данная предпосылка выполняется, то условие первого порядка позволяет определить действительно максимум, а не минимум функции.

28(4).

Отсюда имеем:

Таким образом, экономический смысл условия первого порядка очевиден: в точке оптимального выбора предельная норма замещения одного блага другим из потребительского набора должна быть равна соотношению цен этих двух благ.