Моменты инерции

Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.

Момент инерции относительно точки

Скалярная величина

или

называется полярным моментом инерции относительно точки О. d – расстояние от текущей точки до точки О.

Момент инерции относительно оси

Скалярная величина или

называется моментом инерции относительно оси l. r – расстояние от точки до оси.

Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции.

Величина 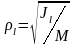называется радиусом инерции.

Момент инерции относительно оси через радиус инерции относительно этой же оси определяется выражением .

Моменты инерции относительно осей координат

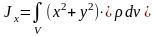
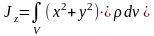
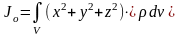
Центробежные моменты инерции

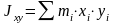
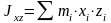
Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс.

Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера)

Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.

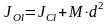
Доказательство: Пусть имеется две декартовы системы координат и 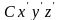, оси которых параллельны. Начало системы находится в центре масс системы. Докажем теорему для осей и .

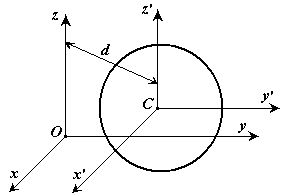
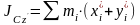
Координаты связаны между собой соотношениями:

, ,

, , .

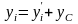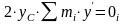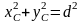Следовательно 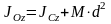, что и требовалось доказать.

Главными осями инерции называются оси, в которых центробежные моменты инерции равны нулю.

Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.

Тензор инерции и тензор инерции для главных осей:

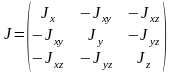
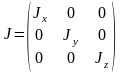
Моменты инерции простейших тел Лекция 4

Краткое содержание: Динамика несвободной материальной точки. Относительное движение материальной точки. Частные случаи.

Динамика несвободной материальной точки

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, которое называется уравнением связи.

Если точка вынуждена двигаться по некоторой линии, то уравнениями связи являются уравнения этой лини.

,

Таким образом, движение несвободной материальной точки зависит не только от приложенных к ней активных сил и начальных условий, но так же от имеющихся связей. При этом значения начальных параметров должны удовлетворять уравнениям связей.

Связи бывают двухсторонние или удерживающие и односторонние или неудерживающие.

Связь называется двухсторонней если, накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве на которых должна находится точка.

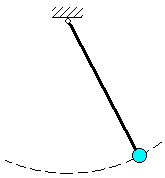
Пример

Материальная точка подвешена на стержне длины .

Уравнение связи имеет вид:

Связь называется односторонней если, накладываемые ею на координаты точки ограничения выражаются в форме неравенств. Односторонняя связь препятствует перемещению точки лишь в одном направлении и допускает ее перемещение в других направлениях.

П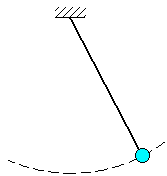 ример

Материальная точка подвешена на нити длины .

Уравнение связи имеет вид: