Условия равновесия плоской системы сил

Необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента. Для плоской системы сил эти условия получают вид F_o=åF_k=0, М_Оz=åМ_oz(F_k)=0, (5.15), где О– произвольная точка в плоскости действия сил. Получим: F_ox=åF_kx=F_1x+F_2x+…+F_nx=0, P_ox=åF_ky=F_1y+F_2y+…+F_ny=0, М_Оz=åM_Oz(F_k)=M_oz(F₁)+M_oz(F₂)+…+M_oz(F_n)=0, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй  формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой; åM_Az(F_k)=0, åM_Bz(F_k)=0, åM_Cz(F_k)=0, (5.17), где A, В и С– указанные точки. Необходимость выполнения этих равенств вытекает из условий (5.15). Докажем их достаточность. Предположим, что все равенства (5.17) выполняются. Равенство нулю главного момента при центре приведения в точке А возможно, либо если система приводится к равнодействую­щей (R≠0) и линия ее действия проходит через точку А, либо R=0; аналогично равенство нулю главного момента относительно точек В и С означает, что либо R≠0 и равнодействующая проходит через обе точки, либо R=0. Но равнодействующая не может про­ходить через все эти три точки А, В и С (по условию они не лежат на одной прямой). Следовательно, равенства (5.17) возможны лишь при R=0, т. е. система сил находится в равновесии. Заметим, что если точки А, В и С лежат на одной прямой, то выполнение условий (5.17) не будет достаточным условием равнове­сия, — в этом случае система может быть приведена к равнодейст­вующей, линия действия которой проходит через эти точки.

1. - Основная форма уравнений равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей и сумма их алгебраических моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю: 
 F_ix = 0; F_iy = 0; M_O(F_i) = 0. (I)

2. Вторая форма уравнений равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно двух центров А и В и сумма их проекций на ось Ox, не перпендикулярную оси Ox, были равны нулю: 
 F_ix = 0; M_А(F_i) = 0; M_В(F_i) = 0. (II)

3. Третья форма уравнений равновесия (уравнения трех моментов): для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно любых трех центров А,В и С, не лежащих на одной прямой, были равны нулю: 
 M_А(F_i) = 0; M_В(F_i) = 0; M_С(F_i) = 0. (III)

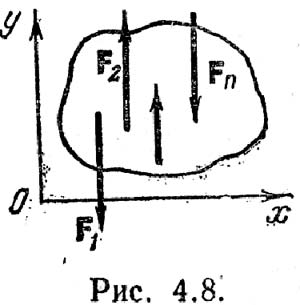
4. - Плоская система параллельных сил. В этом случае, когда все действующие на тело силы параллельны друг другу, можно для удобства направить ось Ox перпендикулярно силам. Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из уравнений (I) обратится в тождество. 
В результате для плоской системы параллельных сил остаются два уравнения равновесия: 
 F_iy = 0; M_O(F_i) = 0. 
Другая форма уравнений для такой системы сил, вытекающая из общих уравнений (II), имеет вид: 
 M_А(F_i) = 0; M_В(F_i) = 0. 
При этом точки А и В не должны лежать на прямой, параллельной силам.

Плоская система сходящихся сил.В этом случае, когда линии действия всех сил пересекаются в одной точке, их моменты относительно этой точки равны нулю. 
В результате получаем следующие уравнения равновесия:
 F_ix = 0; F_iy = 0; 
то есть для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы прекций этих сил на координатные оси Ox и Oy были равны нулю.