
2.3. Момент пары сил
Вектор
момента пары сил ![]() направлен
перпендикулярно плоскости действия
пары сил в ту сторону, откуда вращение
тела парой сил наблюдается происходящим
против часовой стрелки (рис. 2.2).
направлен
перпендикулярно плоскости действия
пары сил в ту сторону, откуда вращение
тела парой сил наблюдается происходящим
против часовой стрелки (рис. 2.2).
Модуль
момента пары сил равен произведению
модуля одной из сил пары на ее плечо, т.
е. ![]() .
.
|
|
Рис. 2.3. Проекции векторного момента пары сил на оси координат
Векторный
момент ![]() пары
сил, произвольно расположенный в
декартовой системе координат
пары
сил, произвольно расположенный в
декартовой системе координат ![]() ,
может быть представлен в разложении
по этим
осям координат (рис. 2.3),
,
может быть представлен в разложении
по этим
осям координат (рис. 2.3), ![]() ,
где
,
где ![]()
![]()
![]() –
проекции векторного момента
–
проекции векторного момента ![]() на
соответствующие оси координат.
на
соответствующие оси координат.
Векторный
момент пары сил, расположенный в одной
из координатных плоскостей, или ей
параллельной, следует приложить в
центре ![]() ,
направив вдоль соответствующей оси в
сторону, откуда вращение тела парой сил
представляется против часовой стрелки
(рис. 2.4). Так
,
направив вдоль соответствующей оси в
сторону, откуда вращение тела парой сил
представляется против часовой стрелки
(рис. 2.4). Так ![]()
![]()
![]() ,
где
,
где ![]()
![]()
![]() –
модули моментов соответствующих пар
сил.
–
модули моментов соответствующих пар
сил.
Билет 4 сучка
Главный вектор и главный момент системы сил. Теорема Вариньона о моменте равнодействующей.
Главный вектор и главный момент плоской системы сил
Р ассмотрим
плоскую систему сил (F1, F2,
..., Fn),действующих
на твердое тело в координатной плоскости
Oxy.
ассмотрим
плоскую систему сил (F1, F2,
..., Fn),действующих
на твердое тело в координатной плоскости
Oxy.
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
... + Fn = ![]() Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1) + MO(F2) + ... + MO(Fn) = MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.
Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
Пример
В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил Fix, Fiy и координаты xi, yiточек их приложения.
Модуль R главного вектора плоской системы сил и его направляющие косинусы ex, eу вычисляются по следующим формулам:
R
= (Rх +
Ry)![]() ;
ex =
Rx /
R; ey =
Rу /
R; Rx =
Fix;
Ry =
Fiy.
;
ex =
Rx /
R; ey =
Rу /
R; Rx =
Fix;
Ry =
Fiy.
Здесь в суммировании проекций можно не включать силы, образующие пары сил (Fk, F'k), Fk = -F'k, поскольку суммы проекций таких двух сил на любую ось равны нулю.
Алгебраический главный момент LO плоской системы сил относительно центра O ( начала координатных осей ) вычисляется по формуле:
LO = (xi Fiy - yi Fix) + Mk.
Здесь во вторую сумму выделены алгебраические моменты Mk пар сил (Fk, F'k).
В случаях, когда плечи hi всех сил определяются достатосно просто ( например, если силы параллельны координатным осям Ox и Oy ), величина LO может быть вычислена по формуле:
LO = ± Fi hi + Mk.
ТЕОРЕМА:
Момент равнодействующей силы относительно любой точки на
плоскости равен алгебраической сумме моментов составляющих сил
относительно той же точки.
Определим момент равнодействующей силы R, приложенной в
точке К, относительно произвольно выбранного центра приведения
О.
Мо(R)=Rh, но R=R* и h=M*/R*
Тогда
Мо(R)=R*/M*R*=M=M1o+M2o+…+Mno
Что и требовалось доказать…
Билет 5 сучка


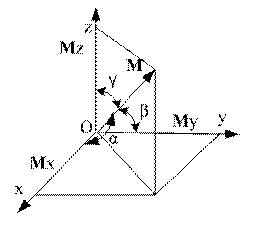
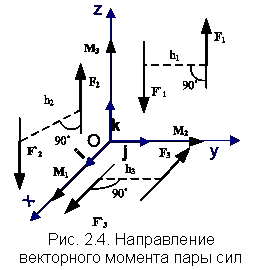 Рис.
2.2. Момент пары сил
Рис.
2.2. Момент пары сил