Билет 1 сучка

1. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, силы внешние и внутренние.

Статика - раздел механики, предметом которого являются материальные тела, находящиеся в состоянии покоя при действии на них внешних сил. В широком смысле слова статика - это теория равновесия любых тел

Абсолютно твёрдое тело – тело, расстояние между частями которого не изменяется при действии на него сил, т.е. форма и размеры твёрдого тела не меняются при действии на его любых сил. Конечно таких тел в природе не существует. Это физическая модель. В тех случаях, когда деформации малы, можно реальные тела рассматривать как абсолютно твёрдые. Движение твердого тела в общем случае очень сложно.

Абсолютно твёрдое тело— тело в котором расстояние между 2 его точками ост. неизменным независимо от действия на него сил.

Под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимо­действующие тела могут сообщать друг другу ускорения или де­формироваться (изменять свою форму).

Сила является векторной величиной. Она характеризуется чис­ленным значением, или модулем, точкой приложения и направлением.

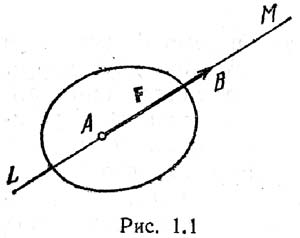
Точка приложения силы и ее направление определяют линию действия силы. На рисунке показано, как сила приложена к точке A. Отрезок AB= модулю силы F. Прямая LM называется линией действия силы. В сист. СИ сила изм. в ньютонах (Н).

Существует 2 способа задания силы: непосредственным описанием и векторный (ч-з проекции на оси координат).

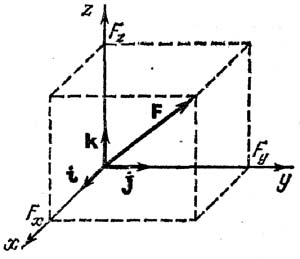
F= Fxi + Fyj + Fzk , где Fx, Fy, Fz– проекции силы на оси координат, а i, j, k - единичные орты

Совокупность нескольких сил (F1, F2, ... ,Fn) называется системой сил.

Если, не нарушая состояния тела, одну систему сил (F1, F2, ..., Fn) можно заменить другой си­стемой (Р1, P 2 , ... , Pn) и наоборот, то такие системы сил называются эквивалентными.

Символически это обозначается следую­щим образом: ( F 1 , F 2 , ... , Fn )~ (Р1, P 2 , ... , Pn).

Однако, это не означает, что если две системы сил оказывают одинаковое действие на тело они будут эквивалентны. Эквивалентные системы вызывают одинаковое состояние системы. Когда система сил ( F 1 , F 2 , ... , Fn ) эквивалентна одной силе R, то R назыв. равнодействующей. Равнодействующая сила может заменить действие всех данных сил. Но не всякая си­стема сил имеет равнодействующую. В инерциальной системе координат выпол­няется закон инерции. Это означает, в частности, что тело, находя­щееся в начальный момент в покое, останется пребывать в этом состо­янии, если на него не действуют никакие силы. Если абсо­лютно твердое тело остается в состоянии покоя при действии на него  системы  сил   ( F 1 , F 2 , ... , Fn ),   то эта система называется   уравно­вешенной, или системой сил, эквивалентной нулю: ( F1 , F 2 , ... , Fn )~0. В этом случае говорят, что тело находится в равновесии. В математике два вектора считаются равными, если они параллельны, направлены в одну сторону и равны по модулю. Для эквивалентности двух сил этого недостаточно и из равенства F=Р еще не следует соотношение F~Р. Две силы эквива­лентны, если они векторно равны и приложены к одной точке тела. 

Абсолютно твердым телом (или неизменяемой механической системой) называется материальное тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между любыми двумя его точками остается постоянным.

Cила - это основная количественная мера механического воздействия одного тела на другое, которая характеризует его интенсивность и направление.

Природа силы может быть различной. Это могут быть гравитационные, электромагнитные, упругие силы или силы давления. Теоретическая механика не интересуется природой сил.

Сила определяется точкой приложения, числовым значением и направлением действия, т.е. является векторной величиной.

Модуль силы находят путем ее сравнения с силой, принятой за единицу. Для статического измерения силы служат приборы, называемые динамометрами.

Силу как величину векторную обозначают какой-либо буквой со знаком вектора (например, или ). Для выражения числового значения силы или ее модуля используется знак модуля от вектора или те же буквы, но без знака вектора (например, и или и ).

Системой сил называется группа сил, которые действуют на рассматриваемое тело или (в общем случае) на точки механической системы.

Если линии действия всех сил лежат в одной плоскости, то система сил называется плоской, а если эти линии действия не лежат в одной плоскости, - то система сил называется пространственной.

Системой сил эквивалентной нулю (или уравновешенной системой сил) называется такая система сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.

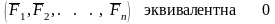
Две системы сил называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях.

Равнодействующей силой рассматриваемой системы сил называется сила, действие которой на твердое тело или материальную точку эквивалентно действию этой системы сил. Равнодействующую силу обозначают обычно

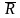
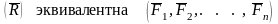
Уравновешивающей силой рассматриваемой системы сил называется сила, добавление которой к заданной системе сил дает новую систему, эквивалентную нулю.

Уравновешенная система сил - это система сил, приложение которой к уравновешенному телу не выводит его из состояния равновесия.

При действии уравновешенной системы сил тело согласно первому закону Ньютона находится в состоянии покоя или движется с постоянной скоростью. Если же система сил является неуравновешенной, нетрудно предположить, что скорость будет изменяться, т.е. появится ускорение. 

Совокупность сил, действующих на любое тело, называется системой сил.

Если одну систему сил,  действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Система сил, под действием  которой свободное твердое тело может находиться в покое, называется уравновешенной.

Равнодействующая – это  сила, которая одна заменяет действие данной системы сил на твердое тело.

 

Внешними силами механической системы называются силы, с которыми на точки и тела механической системы действуют точки и тела не входящие в рассматриваемую систему.

Равнодействующая всех внешних сил приложенных к точке обозначается (от латинского exterior - внешний).

Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы.

Равнодействующая всех внутренних сил приложенных к точке обозначается 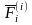(от латинского interior - внутренний).

Это разделение является условным и зависит от того, какая механическая система рассматривается.

Внутренние силы системы обладают следующими свойствами:

Теорема. Главный вектор всех внутренних сил системы (векторная сумма) равен нулю при любом состоянии системы. .

Доказательство: Согласно одной из аксиом динамики, любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.

Теорема. Главный момент всех внутренних сил системы (векторная сумма) относительно любой точки или оси равен нулю при любом состоянии системы. 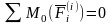или .

Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.

Билет 2 сучка

1. Геометрический и аналитический способы сложения сил. Геометрические и аналитические условия равновесия сходящихся сил. Равновесие трех непараллельных сил.

Тема 3. Сложение сил на плоскости

    С истема сил, линии действия которых лежат в одной плоскости называется плоской.

    Геометрический способ сложения сил. Геометрическая сумма (главный вектор) системы сил F₁, F₂, ..., F_n определяется построением силового многоугольника. Для этого пользуются правилом сложения векторов. В произвольной точке О вектор R, соединяющий начало первого вектора F₁ с концом последнего F_n изображает геометрическую сумму или главный вектор слагаемых сил:

R = F₁ + F₂ + ... + F_n = F_k.     (k = 1, 2, .., n)

   Проекция силы на ось

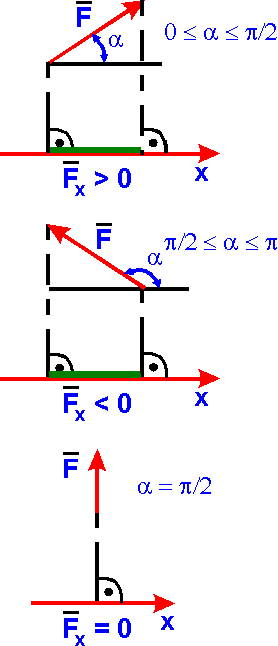     Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси:

FхFcos

F_х> 0, если 0 <  < /2;

 

F_х< 0, если /2 <  < 

 

 

F_х= 0, если   = /2.

    Аналитический способ задания сил на плоскости

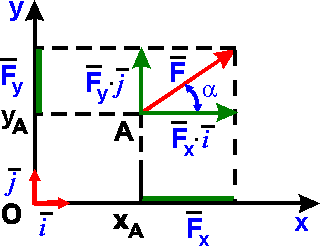
    Силу F на плоскости Оxy можно задать через ее проекции F_хи F_уна оси прямоугольной системы координат по правилу сложения векторов, определив точку А (x_A, y_A) приложения силы:

F  = F_хi + F_уj,

где i, j - единичные векторы. Модуль силы F и углы, которые она образует с координатными осями вычисляются по формулам:

F = [Fх2+ Fу2 + Fz2]1/2; cos (F, i) = Fх/F, cos (F, j) = Fy/F.

     Аналитический способ сложения сил

     Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.Спроецируем равенство R = F_k на оси прямоугольной системы координат Оху, получим

Rх = Fkx,   Ry = Fky,   (k = 1, 2, .., n)

где F_kx, F_ky - проекции k-ой силы F_k на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор R равные геометрической сумме слагаемых сил F₁, F₂, ...,F_n определяется по формулам:

R   = Rхi + Rуj; R = [Rх2+ Rу2]1/2; cos (R, i) = Rх/R,    cos (R, j) = Rу/R.

2.2.

Аналитически способ задания и сложения сил

Выберем систему координат Oxyz. Вектор   можно построить, зная модуль   и углы  между вектором и соответствующими осями

Задание этих величин и определяет силу  . Точка приложения силы должна быть задана дополнительно координатами х, у, z. Кроме того, силу можно задавать проекциями на оси  . Тогда

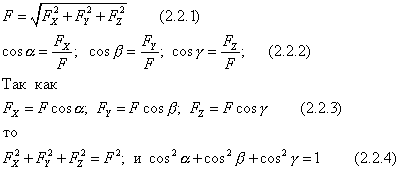
Эти формулы позволяют, зная проекции силы на оси координат найти ее модуль и углы с осями, т.е. определить силу. Зная проекции, можно построить вектор геометрически.

Для плоскости формулы (2.2.1) и (2.2.2) запишутся

Построение в плоскости производится по 4-й аксиоме статики.

Рассмотрим теперь аналитический способ сложения сил. Зависимость между векторами и их проекциями дает следующая теорема:

Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось

Данные соотношения позволяют складывать силы аналитически. Можно заметить идентичность формул (2.2.1)-(2.2.4) и (2.2.9)-(2.2.11).

Решение задач в статике часто связано с операцией сложения из векторной алгебры. Вспомним старые приемы и введем некоторые определения.

Величина, равная геометрической сумме сил какой-либо системы, называется главным вектором системы.

Геометрическую сумму сил не следует смешивать с равнодействующей. Для многих систем сил равнодействующей не существует, а главный вектор можно вычислить для любой.

Рассмотрим сложение двух сил на плоскости. Геометрическая сумма   сил   находится по правилу параллелограмма построением силового треугольника

Модуль R равнодействующей определяем как сторону   треугольника  :

углы   находим по теореме синусов, учитывая, что  , получаем

В продолжение геометрического способа сложения сил, напомним о сложении трех сил не лежащих в оной плоскости.

Геометрическая сумма   трех сил  , не лежащих в одной плоскости изображается диагональю параллелепипеда, построенного на этих силах ( Здесь необходимо подчеркнуть полную аналогию рисунков 14 и 17, где в роли   выступает  , а в роли   соответственно  . Coответственно мы можем использовать формулы (2.2.1-2.2.4).

Рассматривая плоскую систему сходящихся сил необходимо рассмотреть и положение такой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется построением силового многоугольника или последовательным сложением сил системы. Пусть дана система   сходящихся сил

Для построения силового многоугольника выбираем произвольную точку О и переносим в нее начало  , затем переносим в конец вектора   начало   и т.д. после переноса вектора   конец вектора будет в некоторой точке N. Соединяем точки О и N вектором  . Этот замыкающий вектор и будет главным вектором системы.

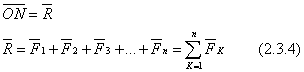
При последовательном сложении сил (рис. 18, а) все они переносятся вдоль линий действия в точку пересечения А. Последовательно, по правилу параллелограмма, складываются силы   получается вектор  :

который представляет собой равнодействующую, равную главному вектору всех сил и приложенную в точке их пересечения.