2.3. Выборочная функция распределения.

Чтобы от отдельных событий перейти к одновременному рассмотрению многих событий, используют накопленную частоту. Так называется отношение числа единиц, для которых результаты наблюдения меньше заданного значения, к общему числу наблюдений. (Это понятие используется, если результаты наблюдения – действительные числа, а не вектора, функции или объекты нечисловой природы.) Функция, которая выражает зависимость между значениями количественного признака и накопленной частотой, называется выборочной (эмпирической) функцией распределения.

Определение 2.9. Выборочной (эмпирической) функцией распределения называется относительная частота события X<x, полученная по выборке: <x). Эмпирическая функция распределения содержит всю информацию о результатах наблюдений. Чтобы записать выражение для эмпирической функции распределения в виде формулы, введем функцию с(х, у) двух переменных:

(2.6)

Случайные величины, моделирующие результаты наблюдений, обозначим . Тогда эмпирическая функция распределения F_n(x) имеет вид

(2.7)

Из закона больших чисел следует, что для каждого действительного числа х эмпирическая функция распределения F_n(x) сходится к функции распределения F(x) результатов наблюдений, т.е. F_n(x) → F(x)   (2.8)

при n → ∞. Советский математик В.И. Гливенко (1897-1940) доказал в 1933 г. более сильное утверждение: сходимость в (2.7) равномерна по х, т.е.

   (2.9)

при n → ∞ (сходимость по вероятности). Здесь использовано обозначение sup (читается как «супремум»). Для функции g(x) под  понимают наименьшее из чисел a таких, что g(x)<a при всех x. Если функция g(x) достигает максимума в точке х₀, то . В таком случае вместо sup пишут max. Хорошо известно, что не все функции достигают максимума. В том же 1933 г. А.Н.Колмогоров усилил результат В.И. Гливенко для непрерывных функций распределения F(x). Рассмотрим случайную величину

(2.10)

и ее функцию распределения По теореме А.Н.Колмогорова при каждом х, где К(х) – функция распределения Колмогорова.

Рассматриваемая работа А.Н. Колмогорова породила одно из основных направлений математической статистики – непараметрическую статистику. И в настоящее время непараметрические критерии согласия Колмогорова, Смирнова, омега-квадрат широко используются. Они были разработаны для проверки согласия с полностью известным теоретическим распределением, т.е. предназначены для проверки гипотезы . Основная идея критериев Колмогорова, омега-квадрат и аналогичных им состоит в измерении расстояния между функцией эмпирического распределения и функцией теоретического распределения. Различаются эти критерии видом расстояний в пространстве функций распределения. Аналитические выражения для предельных распределений статистик, расчетные формулы, таблицы распределений и критических значений широко распространены, поэтому не будем их приводить. По упорядоченной статистической совокупности типа таблицы 2.2 можно построить выборочную функцию распределения:

(2.11)

Функция F*(x) – разрывная ступенчатая функция, непрерывная слева, равная нулю левее наименьшего наблюдённого значения случайной величины Х и единице – правее наибольшего. Теоретически она должна иметь n скачков, где n – число опытов, а величина каждого скачка должна быть равна 1/n – частоте наблюдённого значения случайной величины Х. Практически, если одно и то же значение наблюдалось несколько раз, соответствующие скачки сливаются в один, так что общее число скачков равно числу различных наблюдённых значений случайной величины. Каждый скачок в точке равен «кратности» значения в статистической совокупности, делённой на число опытов n. График выборочной функции распределения называют кумулятой (линия накопленных относительных частот).

Например, для данных таблицы 2.3 статистическая функция распределения F*(x) ведёт себя следующим образом: до точки х= 75 (и включая её) она равна нулю; в ней она совершает скачок, равный 1/n = 0,01 и сохраняет значение 0,01 до точки х = 80 (включая её); здесь она делает скачок, равный 2/n = 0,02, становится равной 0,03 и сохраняет это значение до точки х = 82 (включая её) и так далее. Вычисляя таким образом функцию F*(x), получают таблицу её значений на интервалах между скачками (таблица 2.3).

Таблица 2.3 Таблица значений статистической функции распределения

х	F*(x),	х	F*(x),
x<75 75<x<80 80<x<82 82<x<84 84<x<85 85<x<87 87<x<88 88<x<89 89<x<90 90<x<91 91<x<92 92<x<93 93<x<94 94<x<95 95<x<96 96<x<97 97<x<98 98<x<99 99<x<100 100<x<101	0 0,01 0,03 0,05 0,06 0,07 0,09 0,14 0,15 0,17 0,20 0,24 0,26 0,29 0,35 0,37 0,41 0,43 0,48 0,52	101<x<102 102<x<103 103<x<104 104<x<105 105<x<106 106<x<107 107<x<108 108<x<109 109<x<110 110<x<111 111<x<112 112<x<115 115<x<116 116<x<118 118<x<120 120<x<121 121<x<122 122<x<123 123	0,58 0,64 0,66 0,68 0,70 0,72 0,74 0,77 0,78 0,80 0,84 0,86 0,89 0,91 0,93 0,95 0,96 0,99 1,00

По материалам этой таблицы может быть построен график функции F*(x), по которому можно сделать представление о характере распределения случайной величины Х; разумеется, самое общее представление, так как ясно, что некоторые особенности кривой F*(x) случайны и связаны с выбором именно тех, а не других сопротивлений для измерения. Другие 100 опытов дали бы несколько иной график функции F*(x), но общая тенденция сохранилась бы. При неограниченном увеличении n скачки кривой F*(x) станут более мелкими, кривая станет плавнее и будет приближаться (сходиться по вероятности) к функции распределения случайной величины Х. На рис. 2.1. показан пример такого графика для выборки объёма, равного 16, который называют кумулятой.

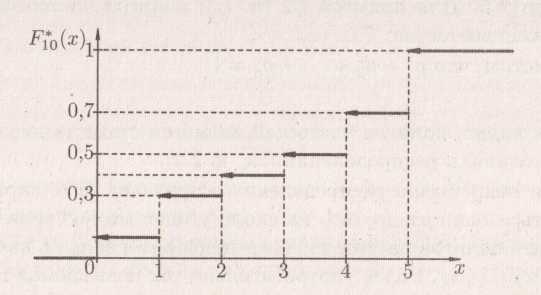
Рис. 2.1. Кумулята (график выборочной функции распределения)

Этот способ является довольно трудоёмким и на практике применяются другие, более простые способы построения законов распределения случайных величин по опытным данным.