2. Диагностические параметры и модели

В зависимости от решаемых диагностических задач и конструктивных особенностей объектов используются различные диагностические параметры и модели.

Наибольшую информацию о техническом состоя­нии объекта позволяет получить оценка закона распре­деления вероятности его проводимости или сопротивле­ния. Опыт использования такой оценки известен в три­бометрии при определении нагрузки в контакте, интен­сивности изнашивания, исследовании явления пленочно­го голодания. Оценка закона, однако, представляет су­щественную проблему и предполагает применение сложной диагностической аппаратуры, что приемлемо лишь в лабораторных условиях при проведении триболо­гических исследований. В практике неразрушающего контроля и технической диагностики обычно ограничиваются анализом совокупности диагностических пара­метров - точечных оценок закона распределения вероятности информативного параметра.

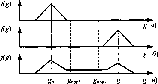
Рис. 19. Плотность распределения проводимости трибосопряжения при жидкостной (а), граничной (б) и полужидкостной (в) смазках

Одним из наиболее распространенных диагностиче­ских параметров является среднее сопротивление, кото­рое определяют либо непосредственно R_cp, либо как ве­личину, обратную средней проводимости R '_ср = 1 / G_cp. В первом случае объект подключают к источнику тока I₀ и измеряют среднее значение падения напряжения U_ср на нем за некоторое время Т_н, а во втором - к источнику напряжения U₀ и измеряют среднее значение тока I_ср:

По существу R_ср и G_cp являются оценками матема­тического ожидания законов распределения вероятности сопротивления и проводимости объекта, поэтому пара­метры R_ср и R'_cр однозначно и комплексно характеризу­ют его состояние. В случае жидкостной смазки (G_cp = g_n) они характеризуют усредненное значение толщины пленки в зонах трения, при граничной (G_cp = g_K) - несут информацию о размерах пятен контактов и толщине по­верхностных пленок. Широкое применение этих пара­метров обусловлено также простотой их измерения (достаточно использовать вольтметр или амперметр с магни­тоэлектрической системой).

На основе совместного рассмотрения теорий фрик­ционного изнашивания, контактирования шероховатых поверхностей и электрического контакта синтезирован универсальный диагностический параметр G''_cp, функ­ционально связанный с интенсивностью фрикционного изнашивания:

где а_с - определяется типом объекта, свойствами мате­риалов деталей, параметрами микрогеометрии рабочих поверхностей, видом смазки.

Так, например, для упругого контакта неровностей поверхностей стальных деталей при режиме смазки, близком к граничному (нагрузку воспринимают в основ­ном микронеровности, а сближение поверхностей опре­деляется нагрузкой в контакте), рекомендуется в зависи­мости от характеристик поверхностей _с €[0,9; 1,1] для точечного контакта и _G € [1,3; 1,7] для линейного контакта; при полужидкостном режиме смазки с редкими микроконтактами (нагрузку воспринимает в основном смазочный слой, сближение определяется толщиной гид­родинамической пленки) рекомендуется _G € [2,9; 3,6]. ­ В случае пластического контакта микронеровностей по­верхностей при граничном трении для точечного контак­та _G = 0,8, для линейного _G = 1,2, а при полужидко­стном режиме смазки с редкими микроконтактами - _G = 2,6. Таким образом, широко применяемый диагно­стический параметр G_cp является частным случаем пара­метра G"_p при _G =1

Характерно, что всегда выполняется условие (R'_ср / R_cр) < 1, при этом знак равенства соответствует g(t) = const, что применительно к жидкостной смазке означает отсутствие колебаний толщины пленки в зонах трения (идеализированная ситуация). Это свойство па­раметров заложено в основу метода оценки степени флуктуаций толщины пленки в зоне трения по диагно­стическому параметру k_n = R'_ср / R_cр, а также метода про­гнозирования состояния подшипников качения в условиях жидкостной смазки по параметру β _д = (R'_ср / R_cр)³. Изме­няясь от 1 при отсутствии колебаний толщины пленки до 0 при полужидкостной смазке, β _д характеризует относи­тельное снижение долговечности подшипника по срав­нению с его долговечностью при той же средней толщи­не пленки и отсутствии ее колебаний.

Для решения ряда трибометрических задач при ра­боте объектов в условиях полужидкостной смазки (оцен­ка средней толщины смазочной пленки в зонах трения, степени ее флуктуаций, размеров действительных пло­щадок контактов при микроконтактировании и т.п.) в качестве диагностических параметров применяются оценки среднего сопротивления смазочной пленки R_n и среднего контактного сопротивления объекта R_K, кото­рые определяют с учетом принятых на рис. 17 обозначе­ний из выражений:

:

где «n_Т - число импульсов проводимости в объекте, соот­ветствующих R(t) ≤ R_пор за время Т_н; t_н(к) - время начала (конца) i-го импульса проводимости; R_nop - пороговое значение сопротивления (задается R_nop € [50; 100] Ом, что несколько превышает сопротивление объекта при микроконтактировании и соответствует g_пор= g_пор1 на рис. 19).

Для контроля и диагностики узлов трения, количе­ственной оценки состояния смазки в зонах трения, де­фектоскопии рабочих поверхностей широко применяются электроконтактные методы, основанные на анализе параметров импульсов проводимости объекта при мик­роконтактировании. В качестве диагностических пара­метров используют предельные и средние значения час­тоты и длительности микроконтактирований за опре­деленное время или число оборотов подвижной детали. Наиболее универсальным и информативным параметром этой группы является нормированное интегральное вре­мя (НИВ) электрического контактирования (К). Значе­ние этого параметра определяется отношением суммар­ной длительности соответствующих микроконтактиро­ванию импульсов проводимости объекта за время измерения к значению Т_н :

Изменяясь от 0 при жидкостной смазке до 1 при граничной смазке параметр НИВ (К) является статисти­ческой оценкой вероятности микроконтактирования в объекте (Р_к).

Электроконтактные методы традиционно исполь­зуются в трибологии для выявления и анализа металли­ческого контактирования деталей трибосопряжений, количественной оценки полужидкостной смазки и т.п., при этом наибольшее развитие эти методы получили в направлении диагностирования подшипников и опор качения.

Обобщенная диагностическая модель микроконтактирования в подшипнике имеет вид:

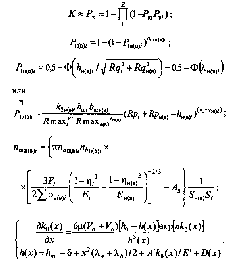
где индексы н(в), i свидетельствуют о принадлежности параметра наружному (внутреннему) кольцу и (или) i-ому телу качения; Р₁ и Р - вероятности микроконтак­тирования деталей по одной паре неровностей и общая; п_ш - число неровностей в зоне контакта; Rq, Rmax, Rp,S, b_ш, v, k₂ - параметры шероховатости поверхностей; λ - коэффициент толщины пленки; F, F_r - общая и ра­диальная нагрузка в контакте; E, η - модуль упругости и коэффициент Пуассона материалов деталей; Σр - сумма главных кривизн поверхностей в точке касания; п_а, n_b - конструктивные параметры подшипника; А_Д - площадь дефекта; k₀(х), h(х) - гидродинамическое давление и толщина смазочной пленки в точке с координатой х; , μ, п - динамическая вязкость и пьезокоэффициент вязко­сти смазочного материала; δ - сближение поверхностей; λ_а, λ_b - кривизны поверхностей до деформации; h_m1 - наименьшее расстояние между недеформированными поверхностями; h₀ - толщина смазочной пленки в точках экстремумов давления; А' - коэффициент пропорцио­нальности; V_a ,V_b - скорости перемещения поверхностей; s, ε - параметры, определяющие профиль дефекта; D_max, m_Д и х' - параметры глубины, протяженности и смещения дефекта; Т_п(х) - полином Чебышева; R(φ), R₀ - текущее и среднее значения радиуса дорожки каче­ния; φ - угловая координата;Q_k , φ_к- амплитуда и фазо­вый угол k-й гармоники радиуса дорожки качения (к = 1 для эксцентриситета, к = 2 для овальности, к = 3... - для огранки); р - предельный номер учитываемой при анализе гармоники; α - координата ближайшего к F_r тела качения; W и β ,- модуль и аргумент вектора смеще­ния кольца; γ = 2п / Z - угловое расстояние между тела­ми качения; Z - число тел качения; G_δ , G_r - упругая ха­рактеристика и радиальный зазор в подшипнике.

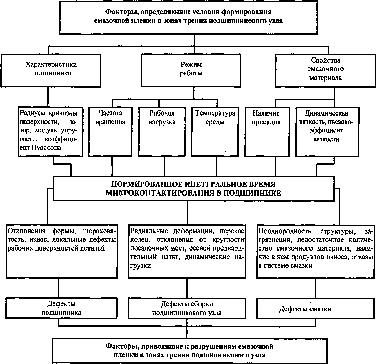
Модель описывает характер влияния на рассматри­ваемый диагностический параметр таких характеристик объекта, как номинальная макрогеометрия, регулярные отклонения геометрической формы, шероховатость и параметры локальных дефектов рабочих поверхностей деталей, свойства конструкционных и смазочных мате­риалов, режимы и условия работы объекта и т.п. (рис. 20). Таким образом, получаемая информация об объекте многопараметрическая, что, с одной стороны, обеспечивает возможность реализации комплексной оценки его состояния, характеризуемого совместным влиянием всей совокупности внутренних параметров объекта и внешних факторов, а, с другой, создает условия контроля отдельных характеристик технического состояния объекта.

При решении задачи выделения необходимой ин­формации о состоянии подшипника принимаются во внимание следующие особенности электроконтактных методов:

• на значение диагностического параметра деталей, которые за время его оценки попадают в контактные зо­ны нагруженных тел качения с кольцами;

• с увеличением нагрузки в контакте вероятность микроконтактирования деталей возрастает, что приводит к увеличению чувствительности параметра к состоянию находящихся в контактной зоне участков рабочих по­верхностей;

• неравномерность распределения нагрузки между телами качения создает возможность задания тре­буемой чувствительности параметра К к различным участкам поверхностей путем их соответствующего нагру­жения.

Рис. 20. Схема воздействия характеристик подшипникового узла на диагностический параметр НИВ

С учетом указанных особенностей выделение необ­ходимой информации о состоянии объекта осуществля­ется путем создания алгоритмов обработки информации о флуктуирующем значении его сопротивления (прово­димости), адаптированных к имеющему место в объекте или создаваемому при диагностировании характеру его нагружения.