1.Дискретизация конструкции.

Рассматриваемая область представляется в виде совокупности конечных элементов, соединенных между собой в узловых точках. Сами элементы могут иметь различную форму и размеры, например, в виде стержня, треугольной пластинки, прямоугольной в плане оболочки, пространственного тетраэдра (рис. 1, а). Выбор типа КЭ и общего их числа зависит от вида и формы конструкции, от требуемой точности, от характера внешней нагрузки и наложенных связей. Например, при расчете стержневых систем каждый стержень постоянного сечения принимается за отдельный элемент (рис. 1, б). Решение в этом случае получается точным.

Дискретизация континуальных систем (пластины, оболочки, массивы) является более сложной задачей. Общих рекомендаций по нанесению сетки или разбивке области на отдельные элементы нет. Обычно руководствуются предварительными представлениями о характере ожидаемого результата и в местах предполагаемых высоких градиентов искомых величин сетку КЭ сгущают. При решении двумерных задач (балка-стенка, изгиб плиты) дискретизация области обычно производится треугольными и прямоугольными элементами (рис. 1, в). Предполагается, что вся действующая нагрузка приводится к узловой, поэтому, например, в случае распределенной нагрузки для ее более точного моделирования бывает необходимо вводить дополнительные узлы и элементы. Заданные перемещения, жесткие или упругие связи также должны быть отнесены к узлам.

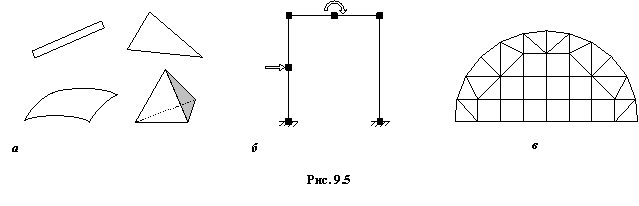
Рисунок 1. Дискретизация конструкции

Таким образом, первый этап заключается в составлении конечно-элементной схемы – дискретной модели конструкции. Здесь можно выделить следующие действия:

а) выбор типа КЭ (по геометрии, виду аппроксимации и т. п.);

б) разбивку области на КЭ (с нумерацией узлов и элементов);

в) описание каждого элемента: топологические (номера узлов в сетке), физико-механические (модуль упругости и т. п.), геометрические характеристики;

г) описание каждого узла (координаты в общей системе координат);

д) описание заданных узловых нагрузок и перемещений.

Несмотря на то, что перечисленные выше действия не опираются на строгие теоретические рекомендации и во многом выполняются интуитивно, первый этап имеет большое значение для дальнейшего расчета конструкции.

2. Построение глобальных матрицы жесткости и вектора узловых сил.

Процедура основана на формировании матрицы жесткости (МЖ) и вектора нагрузок (ВН) отдельных элементов и их размещении в глобальных МЖ и ВН путем обхода по всем конечным элементам дискретной модели.

Расчеты по МКЭ различных конструкций отличаются принципиально только применяемыми элементными МЖ, ВН и матричными операторами для определения внутренних усилий и напряжений. Данные матрицы и векторы строятся на основе вариационных принципов с учетом принятой геометрии КЭ и выбранных аппроксимаций. В случае если МЖ и ВН конечного элемента построены в локальной (местной) системе координат, не совпадающей с глобальной, необходимо преобразовать их для глобальной системы.

Размещение элементных МЖ (ВН) в глобальной МЖ (ВН) может быть выполнено при помощи непосредственного сложения жесткостей.

Таким образом, данный этап включает следующие основные действия, выполняемые в цикле для каждого из конечных элементов:

а) составление элементных МЖ и ВН в локальной системе координат;

б) преобразование элементных МЖ и ВН из локальной в глобальную систему координат – в том случае, если локальная система не совпадает с глобальной;

в) размещение элементных МЖ и ВН в глобальных МЖ и ВН.

Сформированная на этом этапе МЖ системы является вырожденной или особенной. Она может быть преобразована в невырожденную при учете кинематических граничных условий (внешних связей, наложенных на некоторые узлы и исключающих перемещение конструкции как абсолютно твердого тела).