Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .

Вспомним свойства  . Их было два

1. 

2. 

Но учтем теперь что  . Это значит, что    . Тогда имеем следующую цепочку неравенств

Выбрасывая лишнее получим, что     или  , что и говорит о том, что  .

Заметьте, что предел равен как раз супремуму множества  .

Часть 2. Пусть теперь неограниченна сверху. Это значит, что .

Но  . Значит,     и поэтому можно записать    . Выбрасывая в этом неравенстве  , получим окончательно

что и говорит о том, что .

Число e выражается через предел следующим образом:

Это число является трансцендентным и приблизительно равно 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Выполнив подстановку  , где  , получим альтернативную формулу для данного предела:

Здесь мы имеем дело со степенными выражениями, когда и основание и степень стремятся к числу a (или к бесконечности). Во многих случаях такие пределы удобно вычислять, предварительно логарифмируя функцию под знаком предела. 

6. Понятие предельной точки множества и предельной точки последовательности. Теорема о существовании верхнего и нижнего пределов у бесконечного ограниченного множества. Теорема Больцано-Вейерштрасса об ограниченной последовательности.

1. Предельная точка множества. Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р.

Оказывается, в любой окрестности предельной точки содержится бесконечное число точек множества М. Сама же предельная точка может как принадлежать, так и не принадлежать множеству М.

3. Предельная точка числовой последовательности. Так называют (если он существует) частичный предел последовательности {x_n} т.е. такое число с, что существует подпоследовательность {x_nk} данной последовательности, для которой 

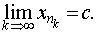
Теорема Больцано-Вейерштрасса

     Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

     Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.

     Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.

     В самом деле, в силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.

     Замечание 2. Пусть {x_n} - ограниченная последовательность, элементы которой находятся в сегменте [a, b]. Тогда предел с любой сходящейся подпоследовательности   также находится на сегменте [a, b].

     Действительно, так как  , то в силу следствия 2 выполняются неравенства a ≤ c ≤ b. Это и означает, что c находится на сегменте [a, b].

     Отметим, что в отдельных случаях и из неограниченной последовательности также можно выделить сходящуюся подпоследовательность. Например, последовательность 1, 1/2, 2, 1/3, ..., n, 1/(n+1), ... неограниченная, однако подпоследовательность 1/2, 1/3, ..., 1/n, ... ее элементов с четными номерами сходится. Но не из каждой неограниченной последовательности можно выделить сходящуюся подпоследовательность. Например, любая подпоследовательность неограниченной последовательности 1, 2, ..., n, ... расходится. Поэтому теорему Больцано-Вейерштрасса, вообще говоря, нельзя распространить на неограниченные последовательности.

7. Фундаментальная последовательность и ее свойства. Критерий Коши сходимости числовой последовательности. Примеры применения критерия Коши.

8. Два определения предела (предельного значения) функции: по Гейне и по Коши, их эквивалентность. Единственность предела функции в данной точке. Односторонние пределы. Бесконечные пределы и пределы на бесконечности.

9. Первый и второй замечательные пределы. Следствия из них. Примеры использования.

10. Арифметические операции над функциями, имеющими пределы.

11. Предельный переход в функциональных неравенствах.

12. Непрерывность функции в точке. Определения непрерывности по Гейне и по Коши. Непрерывность функции в точке слева и справа. Локальные свойства непрерывных функций: ограниченность, сохранение знака.

13. Элементарные функции. Непрерывность простейших элементарных функций. Примеры.

14. Арифметические операции над непрерывными функциями. Суперпозиция функций. Теорема о непрерывности сложной функции.

15. Точки разрыва функции. Их классификация. Примеры.

16. Непрерывность функции на множестве. Свойства функций, непрерывных на отрезке: теоремы о прохождении функции через нуль и через промежуточное значение.

17. Теоремы об ограниченности функции, непрерывной на отрезке (1-я теорема Вейерштрасса) и о достижении такой функцией точных верхней и нижней граней ее значений (2-я теорема Вейерштрасса).

18. Производства функции. Физический и геометрический смысл производной функции. Правая и левая производные функции в точке. Связь дифференцируемости и непрерывности функции в точке.

19. Дифференцирование сложной функции и обратной функции. Производные суммы, разности, произведения и частного двух функций.

20. Формулы дифференцирования простейших элементарных функций. Примеры.

21. Теорема о нуле производной (теорема Ролля).

22. Теорема Лагранжа (формула конечных приращений).

23. Теорема Коши )обобщенная формула конечных приращений).