
- •Вопросы по математическому анализу
- •Числовая последовательность. Предел числовой последовательности. Теорема о единственности предела. Теорема об ограниченности сходящейся числовой последовательности.
- •Бесконечно малые и бесконечно большие числовые последовательности. Их взаимосвязь и свойства. Примеры.
- •Арифметические операции над сходящимися числовыми последовательностями. (хз то ли это)
- •Предельный переход в неравенствах для числовых последовательностей.
- •Теорема о пределе монотонной ограниченной последовательности. Число е.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
Арифметические операции над сходящимися числовыми последовательностями. (хз то ли это)
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых
последовательностей ![]() и
и ![]() называется
числовая последовательность
называется
числовая последовательность ![]() такая,
что
такая,
что ![]() .
.
Разностью числовых
последовательностей
и
называется
числовая последовательность
такая,
что ![]() .
.
Произведением числовых
последовательностей ![]() и
и ![]() называется
числовая последовательность
такая,
что
называется
числовая последовательность
такая,
что ![]() .
.
Частным числовой
последовательности
и
числовой последовательности
,
все элементы которой отличны от нуля,
называется числовая последовательность 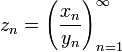 .
Если в последовательности
на
позиции
.
Если в последовательности
на
позиции ![]() всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность
всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность 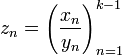 .
.
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
Предельный переход в неравенствах для числовых последовательностей.
Теорема
1. Пусть ![]() -
сходящаяся последовательность и
-
сходящаяся последовательность и ![]() .
Тогда
.
Тогда ![]() .
.
Доказательство этой теоремы проведем методом от противного.
Обозначим ![]() .
Тогда утверждение, противоположное
доказываемому, имеет вид:
.
Тогда утверждение, противоположное
доказываемому, имеет вид:
![]() .
.
Возьмем![]() .
Тогда, по определению, предела
последовательности, можно написать
.
Тогда, по определению, предела
последовательности, можно написать
![]() .
.
Последнее неравенство распишем в виде двойного
![]()
Но
так как
,
то ![]() и
получается что
и
получается что ![]() ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
Следствие.
Если
и ![]() сходящиеся
последовательности и
сходящиеся
последовательности и ![]() ,
то
,
то
![]() .
.
Доказательство дается следующей цепочкой следствий
![]() =>
=> ![]() =>
=> ![]() =>
=> ![]()
=>
Важное
замечание. Допустим, что в условии
теоремы вместо
мы
написали![]() .
Можно ли утверждать, что
.
Можно ли утверждать, что ![]() ?
?
Ответ
отрицательный. Действительно, пусть,
например, ![]() .
Тогда
.
Тогда ![]() ,
но
,
но ![]() .
.
Таким образом, итог этой теоремы и замечание выглядит так: в неравенствах допустим предельный переход, надо только иметь ввиду, что после предельного перехода строгое неравенство (типа > или <) может замениться на нестрогое
(>
перейдет в ![]() ,
< перейдет в
,
< перейдет в ![]() ).
).
Теорема 2. Пусть
и
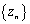 сходящиеся
последовательности;
сходящиеся
последовательности;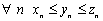 ;
;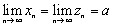
Тогда
также
сходящаяся последовательность и ![]() .
.
Доказательство:
=> ![]()
или ![]()
![]() =>
=> ![]()
или![]() .
.
Беря ![]() и
учитывая, что
и
учитывая, что ![]()
![]() можно
записать
можно
записать ![]()
![]() .
.
Выбрасывая лишнее, получим что
![]() или
или ![]() ,
,
что
и говорит о том, что ![]() .
.
Эту
теорему часто называют “теоремой о
двух милиционерах” (![]() ,
, ![]() -
милиционеры,
-
милиционеры, ![]() -
преступник, которого они “берут в
клещи”).
-
преступник, которого они “берут в
клещи”).
Теорема о пределе монотонной ограниченной последовательности. Число е.
Определение. Последовательность называется
- монотонно
возрастающей (неубывающей), если
![]() ;
;
- строго
монотонно возрастающей (неубывающей),
если
![]() ;
;
- монотонно
убывающей (невозрастающей), если
![]() ;
;
- строго
монотонно убывающей (невозрастающей),
если
![]() ;
;
Монотонно
возрастающие последовательности
обозначают символом ![]() ,
монотонно убывающие - символом
,
монотонно убывающие - символом ![]() .
.
Сейчас докажем одну из важнейших теорем.
Теорема:
1. Если последовательность монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
2.
Если последовательность
монотонно
возрастает, но неограниченна сверху,
то ![]() .
.
Доказательство.
