
- •Вопросы по математическому анализу
- •Числовая последовательность. Предел числовой последовательности. Теорема о единственности предела. Теорема об ограниченности сходящейся числовой последовательности.
- •Бесконечно малые и бесконечно большие числовые последовательности. Их взаимосвязь и свойства. Примеры.
- •Арифметические операции над сходящимися числовыми последовательностями. (хз то ли это)
- •Предельный переход в неравенствах для числовых последовательностей.
- •Теорема о пределе монотонной ограниченной последовательности. Число е.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
Вопросы по математическому анализу
Числовая последовательность. Предел числовой последовательности. Теорема о единственности предела. Теорема об ограниченности сходящейся числовой последовательности.
Определение
1. Если
каждому натуральному числу ![]() по
определённому правилу ставится в
соответствие число
по
определённому правилу ставится в
соответствие число ![]() ,
то множество чисел
,
то множество чисел ![]() называется
числовой последовательностью.
называется
числовой последовательностью.
Определение 2. Числа, из которых составлена последовательность, называют её членами.
Задать
числовую последовательность – значит,
задать правило, с помощью которого по
номеру члена можно найти этот член, т.
е. задать функцию ![]() ,
где
,
где ![]() –
правило соответствия между
–
правило соответствия между ![]() и
,
а
.
и
,
а
.
Определение 3. Общим членом последовательности называется её –й член , записанный в виде функции от , т. е. .
Если
задано,
то последовательность имеет вид ![]() .
Последовательность нельзя задать
указанием нескольких её первых членов.
.
Последовательность нельзя задать
указанием нескольких её первых членов.
Определение 4. Числовая последовательность, у которой все члены равны между собой, называется постоянной последовательностью или просто постоянной.
Пример
1. ![]() ,
т. е.
,
т. е. ![]() .
.
Пример
2. ![]() ,
т. е.
,
т. е. ![]() .
.
Числовая
последовательность – частный случай
дискретной переменной величины ![]() ,
принимающей значение
,
принимающей значение ![]() .
Эта переменная упорядочена, так как
если
.
Эта переменная упорядочена, так как
если ![]() ,
то
,
то ![]() предшествует
.
предшествует
.
Определение
5. Постоянное
число ![]() называется
пределом числовой последовательности
называется
пределом числовой последовательности ![]() ,
если для всякого
,
если для всякого ![]() можно
указать такой номер
можно
указать такой номер ![]() ,
начиная с которого все последующие
члены последовательности удовлетворяют
неравенству
,
начиная с которого все последующие
члены последовательности удовлетворяют
неравенству
![]() .
(1)
.
(1)
Записывается
это так: ![]() при
при ![]() или
или ![]() (читают:
«
стремится
к
при
,
стремящемся к бесконечности, или
предел
при
,
стремящемся к бесконечности, равен
»).
(читают:
«
стремится
к
при
,
стремящемся к бесконечности, или
предел
при
,
стремящемся к бесконечности, равен
»).
Неравенство (1) можно переписать в виде
![]()
Или ![]() .
(2)
.
(2)

Рисунок 1
Определение
6. Интервал
(промежуток) ![]() называется
называется ![]() –
окрестностью точки
.
(рис.1)
–
окрестностью точки
.
(рис.1)
Пользуясь
понятием
–
окрестности, определение предела
числовой последовательности можно
сформулировать следующим образом:
число
есть
предел последовательности ![]() ,
если можно указать такой номер
,
что все члены последовательности с
номерами большими
,
находятся в
–
окрестности точки
,
где
–
любое как угодно малое положительное
число
,
если можно указать такой номер
,
что все члены последовательности с
номерами большими
,
находятся в
–
окрестности точки
,
где
–
любое как угодно малое положительное
число ![]() .
Иначе говоря, все члены последовательности
с номерами, большими
,
на оси
.
Иначе говоря, все члены последовательности
с номерами, большими
,
на оси ![]() (см.
рис.1) изображаются точками, лежащими
от точки
на
расстоянии, меньшем
.
(см.
рис.1) изображаются точками, лежащими
от точки
на
расстоянии, меньшем
.
Определение
7. Последовательность,
имеющая предел, называется сходящейся.![]()
Определение 8. Последовательность, не имеющая предела, называется расходящейся.
Докажем теорему о единственности предела последовательности.
Теорема
1. Последовательность
точек расширенной числовой прямой ![]() может
иметь на этой прямой только один предел.
может
иметь на этой прямой только один предел.
|
Последовательность ![]() называется ограниченной
снизу,
если существует такое число
называется ограниченной
снизу,
если существует такое число![]() ,
что все члены последовательности
удовлетворяют условию
,
что все члены последовательности
удовлетворяют условию ![]() ,
т. е.:
,
т. е.:
![]()
Последовательность называется ограниченной сверху, если:
![]()
Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, т. е. последовательность называется ограниченной, если:
![]()
это можно записать и так:
![]()
Таким образом, последовательность называют ограниченной, если множество ее значений ограничено.
Примеры.
Теорема: ( об ограниченности сходящейся последовательности)
Если последовательность имеет предел, то она ограничена.
Доказтельство:
Пусть
последовательность
имеет
предел, равный а. По
определению предела для ![]() найдем
номер N такой,
что при всех
найдем
номер N такой,
что при всех ![]() имеет
место неравенство
имеет
место неравенство ![]() .
Так как модуль суммы не превосходит
суммы модулей, то:
.
Так как модуль суммы не превосходит
суммы модулей, то:
![]() .
.
Поэтому при всех выполняется неравенство:
![]() .
.
Положим ![]() ,
тогда
,
тогда ![]() при
всех
при
всех ![]() , т.
е. последовательность
ограничена.
, т.
е. последовательность
ограничена.
Замечание: В
силу предыдущей теоремы всякая сходящаяся
последовательность является ограниченной.
Обратное неверно: не всякая ограниченная
последовательность является
сходящейся! Например,
последовательность ![]() ограничена,
но не является сходящейся.
ограничена,
но не является сходящейся.
Замечание: Если условие не выполняется, т. е.
![]() ,
,
то говорят, что последовательность не ограничена.

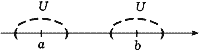 Рис.
49
Рис.
49