7.Определений статических частот изгибных колебаний.

Это частота колебаний лопатки на неподвижном колесе

Частота вращающейся лопатки несколько больше, т.к. центробежная сила стремиться вернуть ее в исходное положение и т.о. как бы ужесточает ее. В этом случае частота собственных колебаний называется динамической – f_д.

При выводе дифференциального уравнения предполагается, что :

а) сила сопротивления колебаниям отсутствует;

б) линейные размеры поперечного сечения лопатки малы по сравнению с ее длинной;

в) колебания происходят в одной из главных плоскостей изгиба

можно воспользоваться уравнением упругой линии

,

где Е – модуль упругости, J(x) – минимальный момент инерции заданного сечения; М (х) – изгибающий момент в этом сечении.

Дважды дифференцируя

,

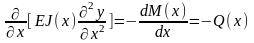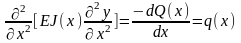
Q(x) – величина поперечной силы в том же сечении,

q(x) – интенсивность нагрузки при колебаниях, она переменна по длине рабочей лопатки и определяется

,

где ρ – плотность, F(x) – площадь; τ- время.

Тогда подставив получим

,

а в нашем случае рабочие лопатки постоянного профиля, т.е. J_х=J=пост. и F=пост. , тогда поучим

,

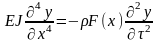поделим обе части на ρF

, где

решение последнего уравнения может быть записано так (Жирицкий Г.С.)

y=Y(Acos λτ+Bsinλτ)

отметим что, уравнение имеет бесконечно большое число решений

но на практике считают опасными первые шесть тонов, для которых запишем:

собственная частота колебаний

.

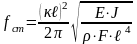8.Определение динамических частот изгибных колебаний.

При отклонении оси рабочей лопатки от радиальной прямой центробежные силы стремятся вернуть лопатку в положение равновесия. Эти силы суммируются с силами упругости и увеличивают жесткость лопатки, а значит и частоту собственных колебаний лопатки. Собственную частоту вращающейся лопатки, называемой динамической частотой, можно оценить по формуле:

,

где n – частота вращения; В – коэффициент, зависящий от геометрических характеристик лопатки и формы колебаний, так для рабочей лопатки постоянного профиля, колеблющихся первом тоне

,

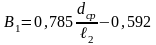или

Для первого тона ,

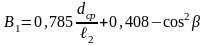где β – угол между окружной R_u b максимальной осью

для второго тона .

9.Определение частот крутильных колебаний

Дифференциальное уравнение крутильных колебаний рабочей лопатки имеет вид:

,

где х - отрезок длины лопатки; GK – жесткость на кручение, G – модуль упругости второго рода, К – геометрическая характеристика жесткости на кручение (для круглого сечения = полярному моменту инерции); φ – угол закручивания; ρ – плотность материала лопатки; J_р – полярный момент инерции сечения лопатки относительно центра тяжести; τ – время.

При гармонических колебаниях φ=φ₀•cosλτ,

где φ₀ – функция, определяющая форму колебаний, λ – круговая частота колебаний (λ=2πf).

Для рабочей лопатки постоянного профиля GK=const. , то тогда исходное уравнение можно преобразовать к виду:

,

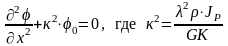выразим λ : .

Тогда частота первого тона крутильных колебаний рабочей лопатки постоянного сечения ,

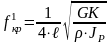Отношение частот: f¹_кр: f²_кр: f³_кр=1 : 3 : 5.