5.2. Идеальные термодинамические циклы двс

Термодинамический цикл ДВС состоит из адиабатного сжатия 1-2 рабочего тела в цилиндре, изохорного 2-3 или изобарного 2-7 подвода теплоты, адиабатного расширения 3-4 или 7-4 и изохорного отвода теплоты 4-1 (рис. 5.3).

В реаль­ных двигателях подвод теплоты осуществляется путем сжигания топлива. В бензиновом ДВС пары бензина перемешаны с необходи­мым для горения воздухом до попадания в цилиндр. Поэтому смесь сгорает в цилиндре практически мгновенно, подвод теплоты оказывается близким к изохорному процессу. В цилиндре дизеля (компрессорного, в настоящее время не выпускаются) сжимается только воздух и затем впрыскивается топливо. Подачу топлива можно отрегулировать таким образом, чтобы давление в процессе его сгорания остается приблизительно посто­янным, и условно можно говорить об изобарном подводе теплоты (цикл Дизеля, не путать с циклом со смешанным подводом теплоты, реализуемом в современных дизелях).

С учетом условий газообмена расширение продуктов сгора­ния в ДВС осуществляют не до атмос­ферного давления р₁ а до более высо­кого давления р₄, а затем открывают выпускной клапан и выпускают горя­чие (с температурой Т₄) продукты сгора­ния в атмосферу. Избыточное давление (р₄ - р₁) при этом теряется бесполезно, В идеальном цикле этот процесс заменяется изобарным отводом теплоты 4-1.

Отношение объема цилиндра v₁ к объему камеры сгорания v₂ называется степенью сжатия двигателя ε. Применительно к идеальному циклу (рис. 5.3):

ε = v₁/v₂. (5.3)

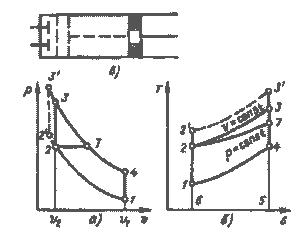
Рис.5.3. Циклы ДВС:

На рис.5.4 для реального двигателя минимальный объем камеры сгорания (объем надпоршневого пространства цилиндра при положении поршня в крайнем верхнем положении, т.е. в ВМТ) обозначен как V_с.

Полный объем цилиндра (объем цилиндра при положении поршня в крайнем нижнем положении, т.е. в НМТ) обозначен как V_а. Этот объем равен:

V_а = V_с + V_h,

где V_h - рабочий объем цилиндра, т.е. объем, который описывает поршень при своем перемещении от ВМТ к НМТ.

Величина V_h определяется очевидным соотношением (площадь поршня на его ход):

V_h = (πD²/4)·S.

Здесь S - ход поршня (расстояние между ВМТ и НМТ), D - диаметр цилиндра.

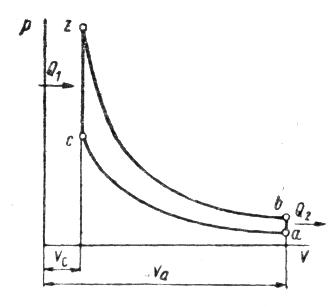
Рис.5.4. Цикл с подводом теплоты при v = const.

С учетом этих соотношений степень сжатия равна:

ε = V_а/V_с = (V_с + V_h)/V_с = 1+ V_h/V_с.

В термодинамическом цикле степень сжатия ε является основным параметром, определяющим термический КПД цикла.

Рассмотрим два цикла (рис.5.3) с одинаковыми точками 1 и 4, один из которых (1׳-2׳-3׳-4) имеет большую сте­пень сжатия ε, чем другой (1-2-3-4). Большему значению ε соответствует бо­лее высокая температура в конце сжатий 1-2.

Следовательно, изохора 2׳-3׳ рас­положена в Т-s диаграмме выше, чем изохора 2-3. Из рис. 5.3-б видно, что количество теплоты q₁, подведенной в цикле 1-2׳-3׳-4 (площадь 2׳-3׳-5-6) больше, чем количество теплоты, подве­денной в цикле 1-2-3-4 (площадь 2-3-5-6). Количество отведенной теплоты q₂ в обоих циклах одинаково (площадь 4-5-6-1). Следовательно, термический КПД η_t = 1 - q₂/q₁ больше в цикле 1-2׳-3׳-4.

Цикл с подводом теплоты при постоянном объеме.

Цикл с подводом теплоты при постоянном объеме реализуется в бензиновых и газовых ДВС с принудительным (искровым) воспламенением заряда. Термический КПД цикла η_t двигателя внутреннего сгорания с подводом теплоты (сгоранием) при v = const при постоянной теплоемкости отыщется как:

.

При одинаковых показателях адиабаты k процессов сжатия и расширения в со­ответствии с (4.18):

; .

Тогда для рассматриваемого цикла:

. (5.4)

Из формулы (5.4) следует, что термический КПД данного теоретического цикла зависит от степени сжатия ε и показателя адиабаты k. На рис. 5.5 приведены кривые зависимости термического КПД цикла со сгоранием при v = const oт степени сжатия при различных показателях адиабаты. На рис.5.6 дается графическое объяснение этому явлению.

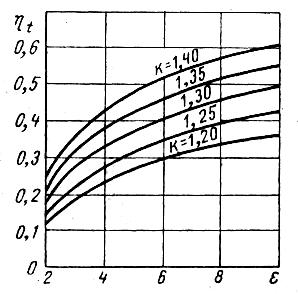
Pис.5.5. Зависимость термического КПД η_t от степени сжатия и показателя адиабаты k для цикла с подводом теплоты при v = const.

Увеличение КПД ДВС с ростом показателя адиабаты k и сте­пени сжатие ε аналитически вытекает из зависимости (5.6) и физически объясняется повышением максимальной темпе­ратуры цикла. Максимальная степень сжатия в бензиновых двигателях ограничивается са­мовоспламенением топливовоздушной смеси (детонацией) и не превышает 9—10. В дизелях, а которых поршень сжимает воздух, величина ε может превышать 16, что позволяет существенно повы­сить КПД цикла.

Однако при одинако­вых степенях сжатия цикл со смешанным подводом теплоты, реализуемый в ди­зелях, имеет меньший КПД, чем цикл с подводом теплоты при v = const, по­скольку при одинаковом количестве от­данной холодному источнику теплоты ко­личество подведенной при v = const (no линии 2-3 на рис. 5.3-6) теплоты больше, чем при р = const (линии 2-7).

При сго­рании при р = const максимальная тем­пература горения, как это видно из рис. 5.3- б, оказывается меньше, чем при v = const.

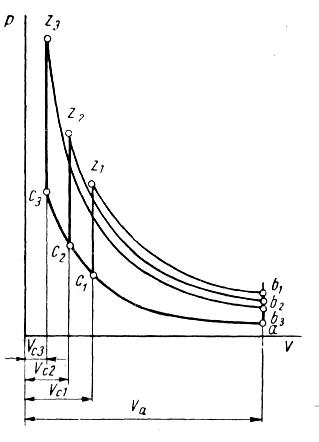
Pис.5.6.Циклы с подводом теплоты при v = const и при различных значениях степени сжатия ε.

Цикл с подводом теплоты при постоянном давлении.

По циклу (цикл Дизеля) с подводом теплоты Q₁ при р = const (рис.5.7) работают двигатели с воспламенением от сжатия и распыливанием топлива сжатым воздухом (компрессорные двигатели). Однако, в настоящее время подобные двигатели не выпускаются из-за громоздкости компрессорной установки и большими затратами энергии на ее привод.

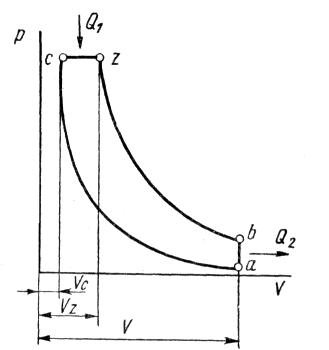
Рис.5.7. Цикл с подводом теплоты при р = const.

Термический КПД этого цикла определяют по формуле, вывод которой приведен ниже («Цикл со смешанным подводом теплоты»):

, (5.5)

где ρ = V_Z/V_C – степень предварительного расширения, то есть отношение удельного объема в конце процесса подвода при р = const к удельному объему в начале этого процесса.

Цикл со смешанным подводом теплоты.

Цикл со смешанным подводом теплоты положен в основу организации рабочего процесса дизелей. В данном цикле теплоту к рабочему телу подводят частично при v = const и частично при р = const (рис.5.8).

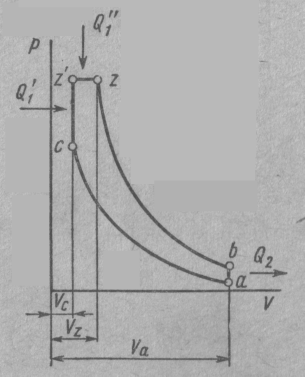
Рис.5.8. Цикл со смешанным подводом теплоты.

Рабочее тело в точке а сжимают адиабатически по линии а-с. Затем к нему подводят теплоту Q₁׳ = с_v(Т_Zۥ - Т_С) по линии с-zۥ при v = const, и теплоту Q₁׳ ׳ = с_р(Т_Z -Т_Zۥ) по линии z-zۥ при р = const. Далее следует адиабатическое расширение рабочего тела по линии z-b и отвод теплоты Q₂ = с_v(Т_b - Т_а) в холодный источник по линии b-а.

Термический КПД смешанного цикла определится как:

. (5.6)

Разделив правую часть выражения (5.6) на с_v, имеем:

(5.7)

Выразим значения температуры в отдельных точках цикла через начальную температуру Т_а . Для адиабаты сжатия а-с:

(5.8)

Для изохоры c-z¹:

(5.9)

Для изобары z¹- z :

(5.10)

Для адиабаты расширения z-b:

(5.11)

Подставляя в уравнение (5.7) значения температур из уравнений (5.8)…(5.11) и произведя соответствующие сокращения, получим выражение для определения КПД цикла со смешанным подводом теплоты:

, (5.12)

где λ=р_z/р_с – степень повышения давления, то есть отношение давления в конце подвода теплоты при v = const к давлению в конце сжатия;

ρ = V_Z/V_C – степень предварительного расширения, то есть отношение удельного объема в конце процесса подвода при р = const к удельному объему в начале этого процесса.

Рассмо­тренные ранее циклы являются частными предельными случаями смешан­ного цикла. Поэтому экономичность и работа этого цикла должны зависеть от всех тех вели­чин, от которых в отдельности зависят эти показатели циклов с подводом теплоты при v = const и при р = const. Влияние отдельных величин, характеризующих цикл, на его экономичность видно из уравнения (5.6), выражающего КПД смешанного цикла. На рис. 5.9 приведены графики зависимости термического КПД смешанного цикла, полученные по уравнению (5.6). Из ана­лиза уравнения следует, что КПД смешанного цикла возрастает с увеличением степени повышения давления λ и падает при росте степени предварительного расширения ρ.

Так как работа в смешанном цикле может изменяться только вследствие изменения λ или ρ, то на основе предыдущего можно сделать следующий вывод: КПД цикла возрастает, если работа за цикл увеличивается из-за роста λ при неизменном ρ, и умень­шается при увеличении ρ при постоянном λ.

Циклы с подводом теплоты при постоянном объеме и при постоянном давлении, как уже отмечалось, можно рассматривать как частные случаи смешанного цикла. Если считать, что объем v_z=v_с и, следовательно, принять ρ = 1, то выражение (5.6) примет вид выражения термического КПД цикла с подводом теплоты при v = const:

.

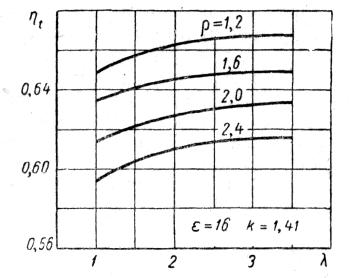
Рис. 5.9. Зависимость к. п. д. смешан­ного цикла от степени повышения давления λ и степени предваритель­ного расширения ρ.

Если же считать, что давление р_z = р_с и, следовательно, λ= 1, это выражение примет вид формулы термического КПД цикла с подводом теплоты при р = const:

.

Исходя из очевидного неравенства:

1 < < (5.13)

можно сделать заключение, что при одинаковых значениях степени сжатия ε цикл со смешанным подводом теплоты имеет меньший термический КПД, чем цикл при v = const. Еще меньше величина термического КПД цикла с подводом теплоты при р = const.

Однако значения степени сжатия карбюраторных и газовых двигателей, работающих по циклу с подводом теплоты при v = const, значительно меньше, чем у дизелей, реализующих цикл со смешанным подводом теплоты. Как следствие этого действительный КПД дизелей (топливная экономичность) выше, чем у бензиновых и газовых ДВС.