1. Построить граф – состояния системы;

2. Расставить потоки, переводящие систему из одного состояния в другое;

3. Записать уравнение Колмогорова для состояния, когда занято 3 канала обслуживания.

Ответ:

1. n=4 m=1

2. 

Задание №28

1. Определение понятия систематическая погрешность.

Ответ:

Систематическая погрешность – это погрешность, которая возникает под действием определенных известных факторов, которая может быть учтена априорно с помощью корректирующих приемов.

2. Что означает моделирование.

Ответ:

Моделирование – это исследование на модели подобной объекту.

3. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.

1. Определить параметр μ– интенсивность потока обслуживания;

2. Построить граф – состояния системы;

3. Записать уравнения Колмогорова, для состояния, когда занято 1 канал обслуживания, n=4.

Ответ:

2. 

Задание №29

1. Определение понятия предельные условия.

Ответ:

Предельные условия – это условия, которые определяют значения характеристик модели на границах, определяющих область её функционирования.

2. Выполняется эксперимент с матрицей планирования 2^n-p.

1. Определить число опытов;

2. Выбрать генерирующие соотношения;

3. Определить определяющий контраст.

Если n=8, p=3.

Ответ:

1. 32 опыта

2. х₅=x₁*x₈

х₆=x₂*x₃

х₇=x₄*x₁

3. 1=x₁*x₈*x₅

1=x₂*x₃*x₆

1=x₄*x₁*x₇

1=x₂*x₃*x₄*x₅*x₆*x₇*x₈

Задание №30

1. Определение понятия идентификация.

Ответ:

Идентификация – это процесс отождествления характеристики объекту или его структуры в их математической модели.

2. Какие объекты называют нерегулярными.

Ответ:

Объекты для дисперсионной меры 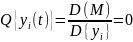(где D(M) – дисперсия условного математического ожидания, 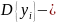общая дисперсия) называются нерегулярными.

3. Автозаправочная станция АЗС представляет собой СМО с 2 каналами обслуживания (2 колонки). Площадка при станции допускает пребывание в очереди на заправку не более 3-х машин одновременно (m=3). Если в очереди уже находиться 3 машины, то очередная машина, пребывшая к станции, в очередь не становится, а проезжает мимо. Поток машин, пребывающих для заправки, имеет интенсивность λ=1 (машина в минуту). Процесс заправки продолжается 1,25 мин.

1. Построить граф – состояния системы;

2. Расставить потоки, переводящие систему из одного состояния в другое;

3. Записать уравнение Колмогорова для состояния, когда занято 2 канала обслуживания.

Ответ:

1. n=2 m=3

2. 

3. 

Задание №31

1. Перечислите виды задач идентификации.

Ответ:

Различают следующие задачи идентификации:

• Параметрическая идентификация, когда структура моделей исследуемого объекта известна с точностью до параметра; тогда необходимо определить неизвестные параметры системы.

• Структурная идентификация – это процесс, который определяет структуру модели исследуемого объекта.

• Структурно-параметрическая идентификация.

2. Виды подобия.

Ответ:

Виды подобия:

• точное;

• приближенное;

• физическое;

• структурное;

• функциональное;

• математическое;

• динамическое;

• вероятностное;

• геометрическое.

3. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.

1. Определить параметр μ– интенсивность потока обслуживания;

2. Построить граф – состояния системы;

3. Записать уравнения Колмогорова, для состояния, когда занято 2 канала обслуживания, n=2.

Ответ:

3.