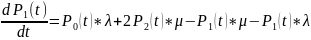Задание №9

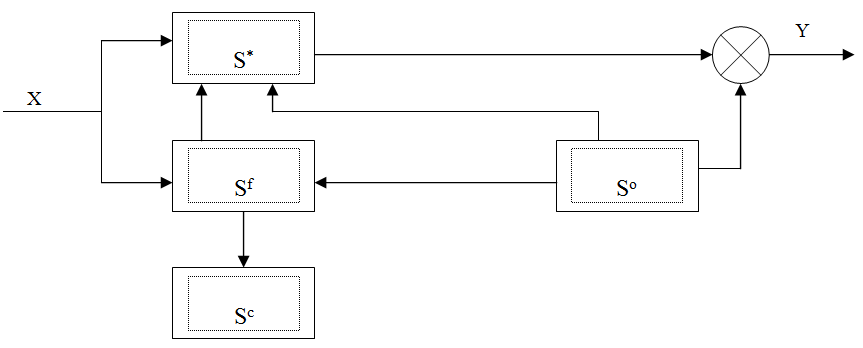
1. Изобразить управляемую и наблюдаемую подсистему многосвязной динамической системы.

Ответ:

Подсистема S* является управляемой и наблюдаемой подсистемой

2. Выполняется эксперимент с матрицей планирования 2^n-p.

1. Определить число опытов;

2. Выбрать генерирующие соотношения;

3. Определить определяющий контраст.

Если n=6, p=3.

Ответ:

1. 8 опытов

2. х₄=x₁*x₃

x₅=x₃*x₂

x₆=x₁*x₂

3. 1=x₁*x₃*x₄

1=x₃*x₂*x₅

1=x₁*x₂*x₆

1=x₄*x₅*x₆

Задание №10

1. Изобразить управляемую и ненаблюдаемую подсистему многосвязной динамической системы.

Ответ:

Подсистема S^f является управляемой и ненаблюдаемой подсистемой

2. Получение ПСЧ. Метод вычетов (конгруентный метод).

Ответ:

3. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.

1. Определить параметр μ– интенсивность потока обслуживания;

2. Построить граф – состояния системы;

3. Записать уравнения Колмогорова, для состояния, когда занято 3 канала обслуживания n=4.

Ответ:

2. 

3. 

Задание №11

1. Изобразить неуправляемую и наблюдаемую подсистему многосвязной динамической системы.

Ответ:

Подсистема S⁰ является неуправляемой и наблюдаемой подсистемой

2. Выполняется эксперимент с матрицей планирования 2^n-p.

1. Определить число опытов;

2. Выбрать генерирующие соотношения;

3. Определить определяющий контраст.

Если n=8, p=4.

Ответ:

1. 16 опытов

2. x₈=x₁*x₂

x₇=x₂*x₃

x₆=x₃*x₄

x₅=x₁*x₄

3. 1=x₁*x₂*x₈

1=x₂*x₃*x₇

1=x₃*x₄*x₆

1=x₁*x₄*x₅

1=x₅*x₆*x₇

Задание №12

1. Изобразить неуправляемую и ненаблюдаемую подсистему многосвязной динамической системы.

Ответ:

Подсистема S^с является неуправляемой и ненаблюдаемой подсистемой

2. Виды моделей. Пример канонической модели.

Ответ:

Виды моделей определяются с видами подобия. Виды подобия:

• точное;

• приближенное;

• физическое;

• структурное;

• функциональное;

• математическое;

• динамическое;

• вероятностное;

• геометрическое.

3. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.

1. Определить параметр μ– интенсивность потока обслуживания;

2. Построить граф – состояния системы;

3. Записать уравнения Колмогорова, для состояния, когда занят 1 канал обслуживания n=2.

Ответ:

2. 

3. 

Задание №13

1. Определение понятия подобие.

Ответ:

Подобие – взаимно-однозначное соответствие между двумя объектами или системами, при котором функции, характеризующие переход от одних параметров к другим, известны, а между математическими описаниями этих двух объектов установлены тождественные отношения.

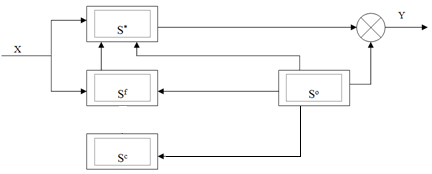
2. Многосвязная динамическая модель.

Ответ:

3. Автозаправочная станция АЗС представляет собой СМО с 3 каналами обслуживания (3 колонки). Площадка при станции допускает пребывание в очереди на заправку не более 1-ой машины одновременно (m=1). Если в очереди уже находиться 1 машина, то очередная машина, пребывшая к станции, в очередь не становится, а проезжает мимо. Поток машин, пребывающих для заправки, имеет интенсивность λ=1 (машина в минуту). Процесс заправки продолжается 1,25 мин.

1. Построить граф – состояния системы;

2. Расставить потоки, переводящие систему из одного состояния в другое;

3. Записать уравнение Колмогорова для состояния, когда занято 3 канала обслуживания.

Ответ:

1. n=3 m=1

2. 

3.