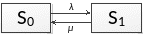Задание №1

1. Определение понятия система по Леону фон Берталанфи.

Ответ:

Система – есть совокупность множества элементов произвольной материальной природы, находящихся в заданных отношениях.

2. Классификация математических моделей элементов сложных систем.

Ответ:

Сложные системы классифицируют по содержательному принципу:

1) САУ;

2) конечные автоматы;

3) вероятностные автоматы;

4) СМО;

и т.д.

3. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.

1. Определить параметр μ– интенсивность потока обслуживания;

2. Построить граф – состояния системы;

3. Записать уравнения Колмогорова, каналов обслуживания n=1.

Ответ:

1. 

2. 

3. 

Задание №2

1. Понятие система по определению Заде.

Ответ:

Системой называется совокупность множества элементов, находящихся в некоторых отношениях с определенными формами взаимодействия.

2. Выполняется эксперимент с матрицей планирования 2^n-p.

1. Определить число опытов;

2. Выбрать генерирующие соотношения;

3. Определить определяющий контраст.

Если n=3, p=1.

Ответ:

1. 4 опыта

2. x₂=x₁*x₃

3. 1=x₁*x₂*x₃

Задание №3

1. Определение понятия сложная система по Юдину.

Ответ:

Сложной системой называется множество взаимодействующих элементов, составляющих нераздельное целое, в котором невозможно точно проследить причинно-следственные связи, определяющие поведение каждого из подмножеств.

2. Канонические модели сложных систем.

Ответ:

Классической канонической моделью системы называется такая упрощенная форма представления системы, которая при данном рассмотрении отображает наиболее общие свойства без потери всеобщности представления о ней.

3. Автозаправочная станция АЗС представляет собой СМО с 3 каналами обслуживания (3 колонки). Площадка при станции допускает пребывание в очереди на заправку не более 1-ой машины одновременно (m=1). Если в очереди уже находиться 1 машина, то очередная машина, пребывшая к станции, в очередь не становится, а проезжает мимо. Поток машин, пребывающих для заправки, имеет интенсивность λ=1 (машина в минуту). Процесс заправки продолжается 1,25 мин.

1. Построить граф – состояния системы;

2. Расставить потоки, переводящие систему из одного состояния в другое;

3. Записать уравнение Колмогорова для состояния, когда система свободна.

Ответ:

1. n=3 m=1

2. 

3. 

Задание №4

1. Определение понятия система согласно Большой Советской Энциклопедии.

Ответ:

Система – (от греческого слова - «состав») нечто составленное из частей и их соединений представляющих собой единство закономерно связанных друг с другом явлений, а также указаний о природе и обществе.

2. Выполняется эксперимент с матрицей планирования 2n-p.

1. Определить число опытов;

2. Выбрать генерирующие соотношения;

3. Определить определяющий контраст.

Если n=5, p=2.

Ответ:

1. 8 опытов

2. x₄=x₁*x₃

x₂=x₅*x₁

3. 1=x₁*x₃*x₄

1=x₅*x₁*x₂

1=x₂*x₃*x₄*x₅

Задание №5

1. Простейшее теоретико-множественное определение понятия система.

Ответ:

Система – есть множество элементов, образующих структуру и обеспечивающих некоторое её поведение в определенной среде.

, где E – множество объектов; sT – структура, объединяющая эти объекты; Q – среда; R(t) – динамика развития.

2. Имеется телефонная линия, в которой заявка – вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потоков вызова λ=0.8 (вызовов в минуту). Средняя продолжительность разговора t_об=1.5(мин). Все потоки событий простейшие.