24.Усилительное /статическое/ звено.

Реальные промышленные объекты регулирования обычно являются весьма сложными системами. Однако в ряде случаев при их исследовании можно не учитывать нелинейные свойства этих объектов и распределенность параметров, т.е. рассматривать их как линейные динамические системы с сосредоточенными параметрами. При таком упрощении любой объект может быть представлен как сочетание определенным образом связанных между собой простейших детектирующих звеньев. Это звено иногда называют также статическим звеном. У=К Х(t) к - коэффициент усиления зяена. Таким образом, выходной сигнал усилительного звена в любой момент времени равен входному сигналу, умноженному ная коэффиц усиления. В качестве примеров усилительного звена можно указать различные усилители, рычажные передачи, редукторы.

OФ: Y(p)=kX(p);

ПФ: W(p)=Y(p)/X(p)=k;

АФХ: W(jω)=k;

АЧХ: P(ω)=k;

ФЧХ: φ(ω)=0;

Таким образом частотные характеристики усилительного звена не зависят от частоты, причем фазо-частотная характеристика тождественно равна нулю, т.е. усилительное звено не изменяет фазы гармонических колебаний, поданных на его вход, а лишь изменяет его по амплитуде в к раз. Амплитудно-фазовая характеристика является положительным действительным числом, следовательно ее график представляет собой точку на положительной ветви действительной оси

25.Интегрирующее звено.

y(t)=Ки∫xdt. Ти* y'(t)=Х (t ), Ти- постоянная времени звена. Ки= 1/Ти Примером интегрирующих звеньев являются различные счетчики, суммирующие расход вещества или энергии за определенный промежуток времени. Другим примером может служить гидравлическая емкость, показанная на. Действительно, если принять в качестве выходной координаты уровень в емкости, а за входную координату - разность между притоком и стоком Оп- Ос , то, так как скорость изменения уровня пропорциональна разности между притоком и стоком жидкости, уравнение гидравлической емкости будет аналогично уравнению.

W(p)=Y(p)/X(p)=Ки/p=1/Тир- перед. ф-я АФХ W(jω)=1/jTω

м(ω)=1/Tk*ω=Ки/ω

ФЧХ: φ=arctgQ/P =arctg(-∞)=-П/2.

Таким образом, амплитудно-частотная характеристика интегрирующего звена является гиперболической функцией частоты, а фазочастотная характеристика не зависит от частоты и равна -П/2. , т.е. в интегрирующем звене выходные гармонические колебания отстают по фазе от входных колебаний на П/2. . Амплитудно-фазовая характеристика является мнимой функцией частоты и годограф АФХ для положительных частот совпадает с отрицательной ветвью мнимой оси.

Переходные характеристики интегрирующего звена можно определить непосредственно из уравнения (2,2) подстановкой соответствующих значений x(t)=1(t) и х(t) = S(t) .Тогда получим: - уравнение кривой разгона

уравнение импульсной переходной функции

Таким образом при подаче на вход интегрирующего звена неисчезающего постоянного возмущения, выходная координата их увеличивается до бесконечности с постоянной скоростью Реакцией же звена на мгновенный импульс единичной площади являет ся ступенчатая функция с амплитудой 1/Ти

26.Идеальное дифференцирующее звено. y(t)=К Х'(t) изменение выходной координаты пропорционально скорости изменения входной координаты. W(p)=Y(p)/X(p)=Кp

W(jω)=К jω

м(ω)=Кω; : φ= П/2.

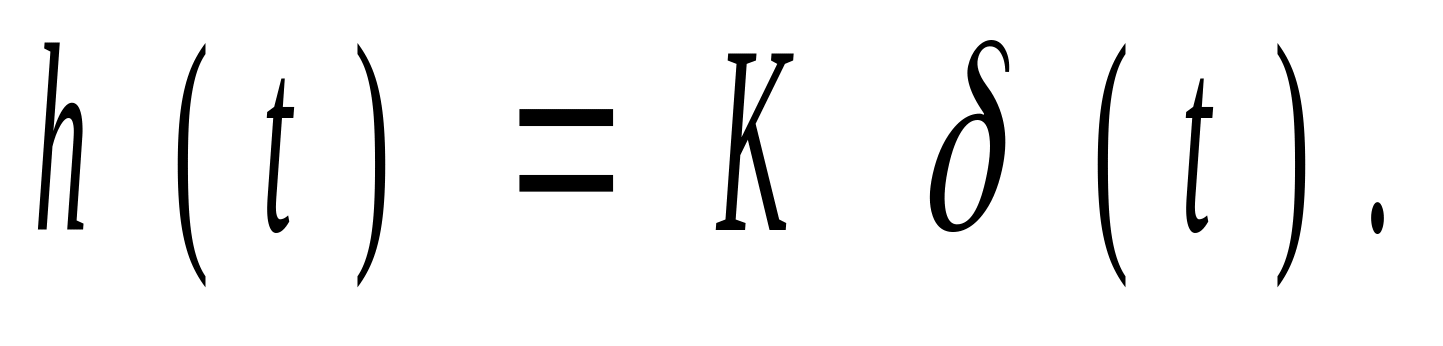
Кривая разгона идеального дифференцирующего звена представляет ообсй 6 -функцию с площадью, равной к .

Примеров идеальных дифференцирующих зпеньев в природе не существует. , как видно из, значение амплитудно-частотной характеристики увеличивается до бесконечности с ростом частоты, это значит, что при постоянной амплитуде входного гармонического сигнала с увеличением частоты увеличивается и амплитуда выходных сигналом. т.е. любой реальный объект практически фильтрует гармонические сигналы с частотой, большей частоты среза данного объекта. Неосуществимость идеального дифференцирующего эвена видна также и из кривой разгона, кото роя является дельта-функцией.