e1.История развития автоматики и теории автоматического управления.

Первый промышленный регулятор был изобретен в 1765 г. И.И. Полэуновым для созданной им паровой машины. Принципиальная схема этого регулятора приведена на рис. 1а. В задачу регулирования здесь входит поддержание в паровом котле постоянного уровня Н . Регулятор представляет собой поплавок I, связанный системой рычагов с регулирующей заслонкой 2. При увеличении уровня поплавок поднимается вверх, в результате чего заслонка опускается, перекрывая трубопровод и уменьшая подачу воды в котел. При уменьшении уровня поплавок опускается, что приводит к увеличению подачи воды и, следовательно,- к повышению уровня.

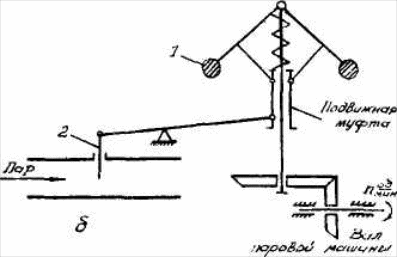
В 1784 г. Джеймсом Уаттом был сконструирован центробежный регулятор числа оборотов вала паровой машины При изменении числа оборотов вала грузы I под действием центробежной силы изменяют свое положение, что приводит к перемещению регулирующего органа 2 и изменению подачи пара. Это в свою очередь вызывает изменение числа оборотов вала, но в направлении, противоположном исходному. Сравнительный анализ рассмотренных регуляторов показывает, что оба они построены по единому принципу.

2.Принцип регулирования Ползунова. Замкнутые системы. Объектами в данных примерах являются паровой котел и паровая машина. К регулирующим устройствам относятся соответственно поплавок и центробежная муфта с регулирующими заслонками. Регулируемые параметры И и п являются выходными сигналами (выходными координатами) объекта, которые мы будем обозначать через у . Технологические параметры, от которых зависят выходные координаты, называются входными координатами (или входами) объекта и обозначаются через -х . Различают возмущающие воздействия х._в (или возмущения), которые вызывают отклонения регулируемого параметра от заданного значения, и регулирующие воздействия х_Р , служащие для поддержания регулируемой координаты на заданном значении. В нашем случае регулирующими воздействиями являются подача воды в паровой котел и расход пара в паровую машину. К основным возмущениям можно отнести в одном случае - давление пара в котле, расход топлива и его теплотворную способность; в другом - нагрувку на валу паровой машины, давление пара в трубопроводе. Общий принцип, по которому построены регуляторы Ползунова и Уатта, состоит в том, что регулятор изменяет регулирующее воздействие при отклонении регулируемой координаты от заданного значения независимо от причин, вызвавших это отклонение. Таким образом, в зависимости от выходного сигнала объекта регулятор изменяет его входной сигнал. Передача сигнала с выхода объекта на его вход называется обратной связью. Поэтому рассмотренный принцип регулирования и называется регулированием по обратной связи или регулированием по отклонению. Системы регулирования, построенные по этому принципу, являются замкнутыми системами.

3.Принцип регулирования Понселе. Разомкнутые системы. При разработке теории центробежных регуляторов хода машин французским ученым Понселе был предложен другой принцип регулирования - по нагрузке на валу машины, которая является одним из основных возмущений в объекте. В этом случае регулирующее воздействие вырабатывается регулятором в зависимости от величины возмущения, а не регулируемого параметра. Отсюда и название этого принципа регулирования - регулирование по возмущению. Системы регулирования по возмущению являются разомкнутыми системами, так как в них отсутствует обратная связь. Идея этого способа регулирования проста: если мы сможем компенсировать все возмущения, то регулируемая величина не будет отклоняться от заданного значения. Недостаток систем, построенных по принципу компенсации возмущений, очевиден: практически в крайне редких случаях нам удается компенсировать все возможные возмущения в объекте. Наличие неетабилизируемых возмущений, таких как колебание атмосферных условий, старение катализатора, закоксовы-вание печей, отложение солей в теплообменниках и т.п., приводит к отклонению регулируемого параметра от заданного значения. Системы регулирования, построенные по принципу обратной связи, не имеют этого недостатка, так как в этом случае регулятор стремится компенсировать отклонение регулируемого параметра от задания независимо от того, какими причинами вызвано это отклонение. Однако при регулировании по отклонению трудно одновременно выполнить условия точности, устойчивости и быстродействия системы. Так, повышение точности и быстродействия системы часто приводит к тому, что система оказывается неработоспособной в силу неустойчивости.

4.Комбинированные системы автоматического регулирования. комбинированные системы автоматического регулирования, сочетающие оба рассмотренных выше принципа. В таких системах основное, наиболее сильное возмущение компенсируется специальным регулятором; кроме того имеется контур регулирования по обратной связи, с помощью которого устраняются отклонения регулируемого па-вызванные другими возмущениями

5.Математическое описание объектов регулирования; уравнения статики и динамики. Число степеней свободы.

Математическое описание объектов регулирования может быть получено экспериментальным, аналитическим или комбинированным экспериментально-аналитическим путем. В первом случае уравнения объекта получают путем постановки специальных экспериментов на объекте (метод активного эксперимента), либо статистической обработкой результатов длительной регистрации координат объекта в условиях его нормальной эксплуатации (метод пассивного эксперимента) . При аналитическом описании уравнения объекта получают на основании анализа физико-химических закономерностей протекающих в нем процессов. Ниже будут даны примеры составления аналитическим путем уравнений некоторых простейших объектов. Экспериментально-аналитический путь получения математического описания объектов подразумевает обычно составление уравнений аналитическим методом с последующим уточнением коэффициентов этих уравнений экспериментальным путем. Уравнения статики описывают установившийся режим, при котором все координаты объекта остаются неизменными во времени, т.е. объект находится в состоянии равновесия. Они представляют собой алгебраические (трансцендентные) или дифференциальные уравнения, содержащие произвсцные по какому-либо параметру, кроме времени. Существенной особенностью уравнений статики является неизменность координат во времени. Уравнения динамики описывают неустановившийся, или переходный режим в объекте: при этом выходная координата объекта является функцией времени и в общем виде уравнение динамики будет дифференциальным уравнением, содержащим производные по времени. Более конкретно вид уравнений статики и динамики определяется характером самого объекта управления и, прежде всего, числом независимых координат, однозначно определяющих состояние объекта в каждый момент времени, которое называется числом степеней свободы объекта . Число степеней свободы характеризует сложность объекта управления, которая далеко не всегда совпадает с его конструктивной сложностью. объекты с сосредоточенными параметрами, которые обладают конечным числом степеней свобода (в том числе достаточно большим); объекты с распределенными параметрами, которые имеют бесконечное число степеней свободы.

6.Уравнение динамики гидравлической ёмкости.

Гидравлическая емкость / представляет собой резервуар, в котором имеется приток и сток жидкости. Основным параметром, характеризующим состояние такого объекта, является уровень жидкости Н , который и выбирается в качестве выходной координаты. При постоянной степени открытия дросселя 2 на стоке жидкости, уровень Н определяется разностью между притоком и стоком Qn~ Q_c . По условиям работы объекта величина притока Qn может произвольно изменяться во времени, поэтому на структурной схеме Qn выбран в качестве входной координаты объекта. Уравнение динамики, описывающее зависимость уровня Н в пе реходном режиме от Qn , получается из известных уравнений гид равлики. обыкновенным нелинейным дифференциальным уравнением 1-го порядка.

7.Линеаризация нелинейных зависимостей

Линейными называются объекты, подчиняющиеся принципу суперпозиции , который заключается в том, что реакция объекта на сумму входных сигналов S^(t) равна сумме реакций на кавдый сигнал в отдельности для любых oci(t) . В частности, линейными являются объекты, описываемые линейными дифференциальными уравнениями, т.е. уравнениями, в которых искомая функция и все ее производные содержатся в первой степени. Следует подчеркнуть, что выполнение принципа суперпозиции необходимо не только в установившихся режимах, но и в переходных процессах. Поэтому линейность статических характеристик является необходимым, но не достаточным условием линейности объекта. эксперимент должен состоять по крайней мере из трех опытов. если нелинейность объекта проявляется в статических режимах и статические характеристики описываются аналитическими функциями, то при определенных условиях нелинейные характеристики объекта могут быть заменены приближенными линейными характеристиками, т.е. производится линеаризация нелинейных зависимостей. Одним из наиболее распространенных способов линеаризации яв ляется разложение нелинейной функции У =• f(X) в ряд Тейлора в окрестности заданной точки (Х_о , У) и переход к новой системе координат х , у , причем линеаризованная функция содержит лишь первые члены ряда Тейлора, линейные относительно новых координат. Пусть статическая характеристика объекта описывается некоторой нелинейной функцией У = f(X)). Предположим, что заданный режим в объекте, который необходимо регулировать, характеризуется точкой А с координатами (Х_о Уо) • При нормальной работе системы регулирования отклонения координат не должны превышать некоторых допустимых значений, определяемых требованиями технологического регламента. Если в пределах этих максимально возможных отклонений X и У от Х_о и У_о f(X) мало отличается от линейной функции, то можно f(X) заменить ее линейным приближением у =f _л(^х) y=f(x+∆x)|_x=x0 =f(x₀)+ (∆x/1!)*f ’(x₀)+ ((∆x)²/2!)*f ’’ (x₀)… ((∆x)ⁿ/n!)*f ⁿ(x₀)

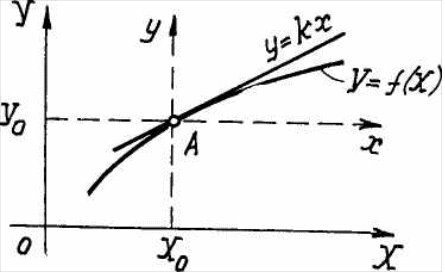
При условии малости разности (Х~Х_О) и ограниченности второй и высших производных от f(X) в выражении можно пренебречь всеми членами, кроме первых двух,: f(x)|_x=x0 ≡f(x₀)+ f ’(x₀)*∆x Переходя к новой системе координат х = Х~Х₀ и у=У~Уо ,получим линеаризованное уравнение объекта:

8.Стационарные и нестационарные линейные объекты; дифференциальные уравнения, описывающие их поведение. Линейные объекты с сосредоточенными параметрами описываются обыкновенными дифференциальными уравнениями, которые в общем случае можно записать в виде: Коэффициенты этого уравнения о_а,... _% а₀ н £_т,.. ., в_о , как это видно из рассмотренных ранее примеров характеризуют конструктивные параметры объекта, физические и химические свойства веществ, а также различные гидродинамические и тепловые константы. Обычно все эти показатели называют "параметрами" объекта (в отличие от входных и выходных координат объекта sc и у ). Различают два типа объектов: стационарные объекты, параметры которых не изменяются во времени, и нестационарные объекты, свойства которых изменяются с течением времени (падение активности катализатора, изменение теплопроводности стенок вследствие отложения солей и т.п.) Стационарные линейные объекты описываются дифференциальными уравнениями с постоянными коэффициентами, нестационарные объекты - дифференциальными уравнениями, коэффициенты которых являются функциями времени. Большинство технологических объектов регулирования являются нестационарными объектами, однако, скорость изменения их свойств намного меньше, чем скорость процессов регулирования этих объектов. Так, например, время регулирования температуры в контактном аппарате производства слабой азотной кислоты составляет несколько минут, а время одного цикла работы катали-затора - несколько месяцев. Такие объекты при расчете системы регулирования можно приближенно рассматривать как стационарные в течение определенного промежутка времени, за который свойства объекта не успевают существенно измениться. Помимо общей формы записи линейных дифференциальных уравнений с постоянными коэффициентами в виде (I.I) в автоматике применяются и другие формы записи. Например, поделив обе части этого уравнения Коэффициенты Т_т, . . ., Та. называются постоянными времени объекта и имеют размерность времени Дифференциальное уравнение объекта описывает его поведение в неустановившихся (переходных) рекимах при любой форме входного сигнала х(1). Уравнение переходного процесса, соответствующее определенному виду функции x(i) , можно получить как решение неоднородного дифференциального уравнения при соответствующей правой части, и заданных начальных условиях. Под начальными условиями переходного процесса понимается его состояние в момент времени, принятый за начало процесса при т=O начальные условия задаются совокупностью значений выходной координаты и ее производных до ( п-1 )-го порядка включительно Начальные условия называются нулевыми, если начальные значения выходной координаты и ее производных все порознь равны нулю

9.Единичная ступенчатая функция и кривая разгона.

Кривая разгона или переходная фукнция Ур (t) которая показывает, как изменяется выходная координата объекта при подаче на его вход сигнала в виде единичной ступенчатой функции 1(t), называемой функцией Хевисайда а_п y⁽ⁿ⁾(t)+ ... +a₁y'(t) + a₀(t) = в_o

x(t)=1(t)={^0,t<0_1,t>0 x(t)- входной сигнал. Обычно кривая разгона объекта определяется экспериментальным путем и используется как исходные данные для расчета системы автоматического регулирования данного объекта.

Рассмотрим для примера гидравлическую емкость (см.рис.6). Предположим, что объект находится в состоянии равновесия, т.е. Qnr Qco =const и, следовательно Н_o= const Подадим на вход объекта ступенчатое возмущение на стоке жидкости, т.е. увеличив резко степень открытия вентиля, изменим скачком сток жидкости от Qn1 до Q_ns2. В результате нарушения материального баланса уровень в резервуаре начнет уменьшаться, что приведет к уменьшению расхода жидкости через вентиль и по окончании переходного процесса в системе установится новое состояние равновесия. Полученный переходный процесс Ур (t) и будет кривой разгона данного объекта.

10.Дельта-функция и импульсная переходная функция.

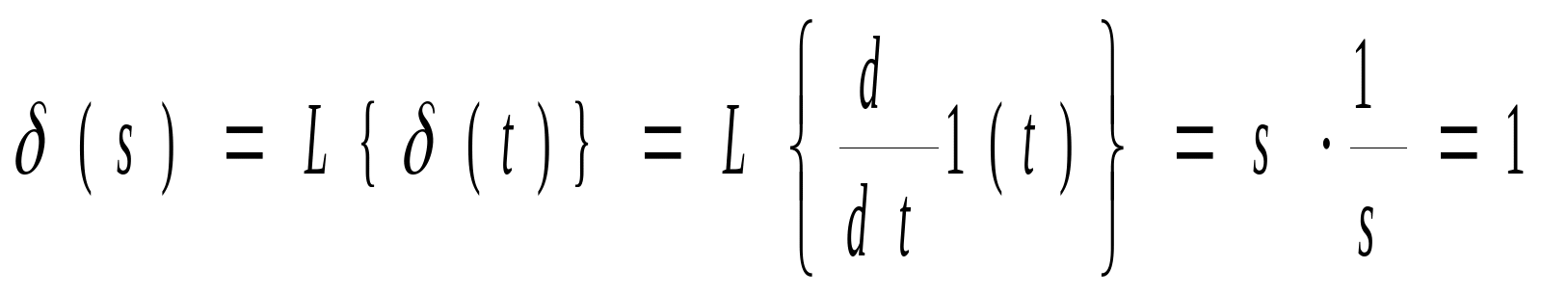
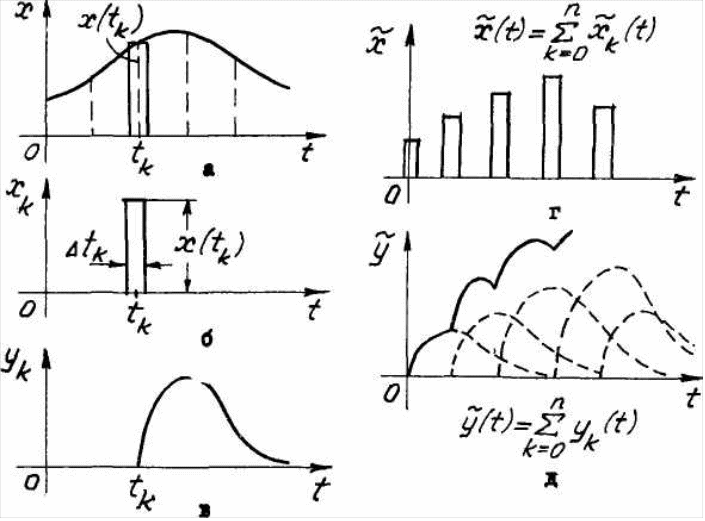
_x(t)=δ(t)={^0,t≠0_∞,t=0

Импульсная переходная функция или весовая функция h(t) показывающая 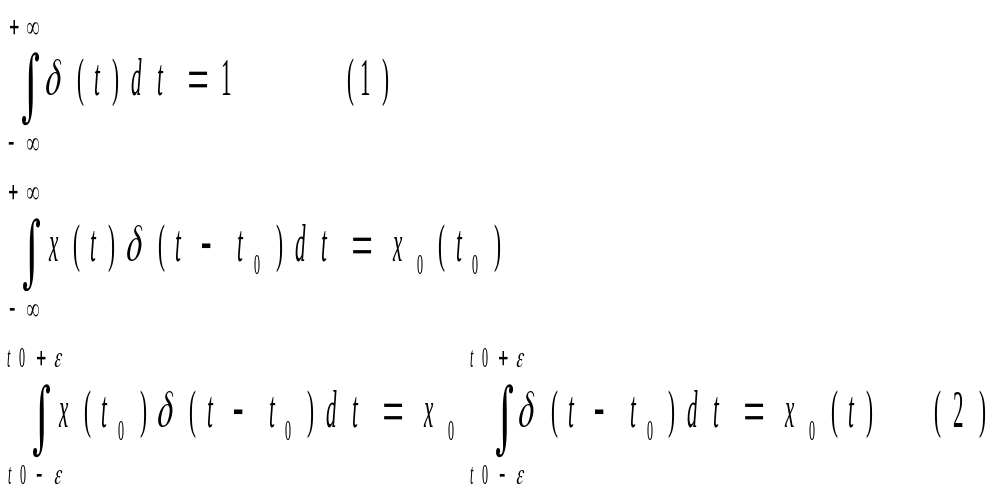реакцию объекта на единичный мгновенный импульс 5(t), называемой дельта-функцией или функцией Дирака

интеграл от произведения какой-либо функции x(t) на дельта-функцию, поданную в момент t_o , равен значению функции в этот момент времени x(t_o ) . Иными словами, с помощью дельта-функции через соотношение (1.5) из непрерывной функции можно "вырезать" одну ординату. Таким образом, дельта-функция представляет собой импульс бесконечно малой длительности и бесконечно-большой амплитуды. Такую функцию можно представить как предел, к которому стремится прямоугольный импульс с основанием ut и с площадью, равной единице (рис.1.4), если основание импульса уменьшать (л1~~О) так, чтобы площадь импульса сохранялась равной ецинипе.

Физической моделью мгновенного импульса, может служить изменение ускорения при соударении абсолютно твердых тел, когда в мо-мент удара скачком изменяются скорости обоих тел. При этом ускорение тела представляет собой мгновенный импульс бесконечно большой амплитуда, а площадь импульса является конечной величиной, определяемой изменением количества движения

тела.