4. Проектирование цилиндрической зубчатой передачи

4.1 Исходные данные

Исходными данными для расчетов параметров цилиндрической зубчатой передачи являются результаты кинематического расчета и значения допустимых контактных и изгибных напряжений.

4.2. Этапы расчета цилиндрической зубчатых передач

4.2.1. Межосевое расстояние

Межосевое расстояние (aw) рассчитывается по формуле

aw ≥Ka(u+1)· ₌ 310,17 (4.1)

Ka – коэффициент, учитывающий тип передачи (для прямозубых Ка=495, для косозубых – Ка=430);

K_Hβ -коэффициент концентрации нагрузки по контактным напряжениям (учитывает неравномерность распределения давления по длине зуба), определяется по таблице 6.2 в зависимости от ѱ_d –величины коэффициента ширины зубчатого колеса по делительному диаметру, который может быть определен по следующей формуле:

Ѱ_d=0,5ψa (u+1) (4.2)

u- передаточное число проектируемой передачи, принимается по результатом окончательной разбивки передаточного числа по ступеням; Т₂ – момент на валу зубчатого колеса, принимается по результатам кинематического расчета;

- допустимые контактные напряжения зубчатой передачи.

4.2.2. Предварительные основы размера колеса

На рис 4.1 представлены основные геометрические параметры цилиндрической зубчатой передачи.

Делительный диаметр колеса (d2) рассчитывается по формуле

d2 , (4.3)

где d2 – мм; аw – мм.

Ширина колеса (b2) -

b2 = ψa * aw (4.4)

Ширина шестерни (b1) –

b1 = b2 + 2…4 мм. (4.5)

Ширину шестерни и колеса после вычисления округляют в ближайшую сторону до стандартного (см. таблицу 6.3).

d2= (2 * 315*4)/(4+1) = 504 мм;

b2 = 0,4 * 504 = 126=125 мм;

b1=130 мм.

4.2.3. Модуль передачи

Модуль передачи m в мм можно ориентировочно рассчитать по формуле

m = (0,01 … 0,02)aw.

m = 6 мм (4.6)

Рассчитанное по формуле (6.6) значение m округляют в ближайшую сторону до стандартного, пользуясь таблицей 6.4.

4.2.4. Модуль передачи

Здесь необходимо отметить, что расчет для косозубых и прямозубых передач аналогичен, так как у последних угол наклона зубьев β=0 .

Рассчитывается минимальный угол наклона зубьев:

косозубые - βmin = . (4.7)

βmin =arcsin 4*6/250=11.1

Далее с учетом βmin определяется суммарное число зубьев шестерни и колеса по формуле

Z∑=2*a_w*cosβmin/m=103.1 . (4.8)

Полученное значение Z∑ округляют в меньшую сторону до целого и определяют для косозубых колес действительное значение угла наклона зубьев

β=arcos=11.47 (4.9)

Для косозубых колес угол наклона должен лежать в пределах от 8 до 18.

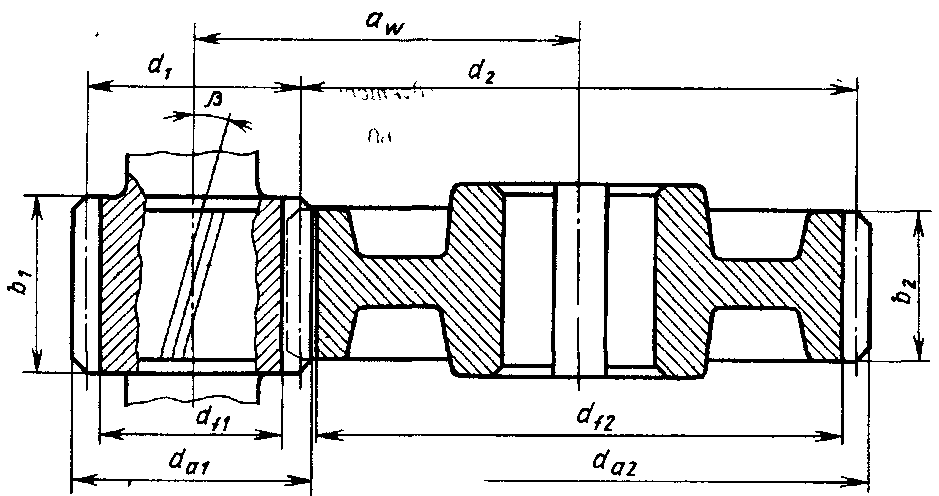
Рисунок 4.1. Геометрические параметры цилиндрической зубчатой передачи

4.2.5. Число зубьев шестерни и колеса

Число зубьев колеса = ≥ =20.6=21. (4.10)

Значение округляют в ближайшую сторону до целого с учетом следующих ограничений:

min = 17 для прямозубой передачи;

z1min = 17 β – для косозубой передачи.

= ; (4.11)

=82.