3.8 Теория ламинарного течения в круглых трубах

Как указывалось ранее, ламинарное течение является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарного течения жидкости основывается на законе трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии в данном случае.

Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d = 2r₀. Чтобы исключить влияние силы тяжести и этим упростить вывод, допустим, что труба расположена горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался (стабилизировался), выделим отрезок длиной l между сечениями 1-1 и 2-2.

Пусть в сечении 1-1 давление равно р₁, а в сечении 2-2 р₂.Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной, а коэффициент а будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечении примет вид

,

где h_тр — потеря напора на трение по длине.

Отсюда

,

ч

Рисунок 3.12 - Схема ламинарного течения жидкости в трубе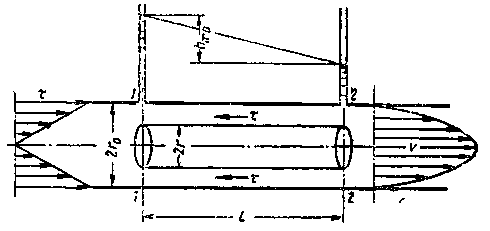

то и показывают пьезометры, установленные в этих сечениях.

В потоке жидкости выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т.е. равенство нулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через τ, получим

откуда

Из формулы следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на рисунке 3.12, слева.

Выразим касательное напряженно τ по закону трения Ньютона через динамическую вязкость и поперечный градиент скорости; при этом заменим переменное у (расстояние от стенки) текущим радиусом r:

Знак минус обусловлен тем, что направление отсчета r (от оси к стенке) противоположно направлению отсчета у (от стенки).

Подставляя значение τ в предыдущее уравнение, получаем

.

Найдем отсюда приращение скорости

При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рисунке 3.12.

Выполнив интегрирование, получим

Постоянную интегрирования С найдем из условия, что на стенке при r = r₀ υ = 0:

,

тогда скорость по окружности радиусом r

. (3.20)

Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени.

Максимальная скорость, имеющая место в центре сечения (при r = 0),

. (3.21)

Входящее в формулу (3.20) отношение p_тр/l (см. рисунок 3.12) представляет собой гидравлический (пьезометрический) уклон, умноженный на ρg. Эта величина является постоянной вдоль прямой трубы постоянного диаметра.

Применим полученный закон распределения скоростей, описываемый уравнением (3.20) для расчета расхода. Для этого выразим сначала элементарный расход через бесконечно малую площадку dS:

Здесь есть функция радиуса, определяемая формулой (3.20), а площадку dS целесообразно взять в виде кольца радиусом r и шириной dr, тогда

После интегрирования по всей площади поперечного сечения, т.е. от r = 0 до r = r₀

(3.22)

Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (3.22) получим

(3.23)

Сравнение этого выражения с формулой (3.20) показывает, что средняя скорость при ламинарном течении в 2 раза меньше максимальной:

Для получения закона сопротивления, т.е. выражения потери напора h_тр на трение через расход и размеры трубы, определим p_тр из формулы (3.22)

Разделив это выражение на ρg, заменив µ на νρ и p_тр на h_трρg, а также перейдя от r₀ к

d = 2r₀, найдем

(3.24)

Полученный закон сопротивления показывает, что при ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, обычно называемый законом Пуазейля, используется для расчета трубопроводов с ламинарным течением.

Заменим в формуле (3.24) расход произведением . После сокращений получим

(3.25)

Данное выражение известно как закон Стокса. Приведем закон сопротивления Стокса к виду формулы Вейсбаха-Дарси:

.

Для этого умножим и разделим формулу (3.25) на , перегруппировав сомножители, после сокращений получим

,

откуда следует, что при ламинарном режиме

. (3.26)

где λ_л — коэффициент потерь на трение для ламинарного течения:

Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением следующих случаев:

1) при течении в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей;

2) при течении с теплообменом;

3) при течении в капиллярах и зазорах с облитерацией;

4) при течении с большими перепадами давления.

Участок от начала трубы, на котором формируется (стабилизируется) параболический профиль скоростей, называется начальным участком течения (l_нач). За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямолинейности и постоянства сечения. Изложенная выше теория ламинарного течения справедлива именно для этого стабилизированного ламинарного течения и неприменима в пределах начального участка.

Рисунок 3.13 - Формирование профиля скоростей на начальном участке

Для определения длины начального участка можно пользоваться приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Re:

. (3.27)

Сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значений производной dυ/dy у стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т.е. чем меньше координата x.

Потеря напора на участке трубы, длина которого l l_нач, определяется по формуле

(3.28)

Закономерности ламинарного течения с теплообменом и большими перепадами давления подробно рассмотрены в [1].