Динамічні показники якості

Найбільше повно динамічні властивості систем виражають перехідні характеристики. Вони задаються технічними вимогами до автоматичних систем. Для систем автоматичної стабілізації, звичайно, задається перехідна характеристика за збуренням , а для систем програмного керування і слідкуючих систем - перехідні характеристики за керуючим впливом h(t).

Перехідні характеристики h(t) (рис. 9.5, а) можуть мати коливальний затухаючий (крива 1) або монотонний (крива2) характер.

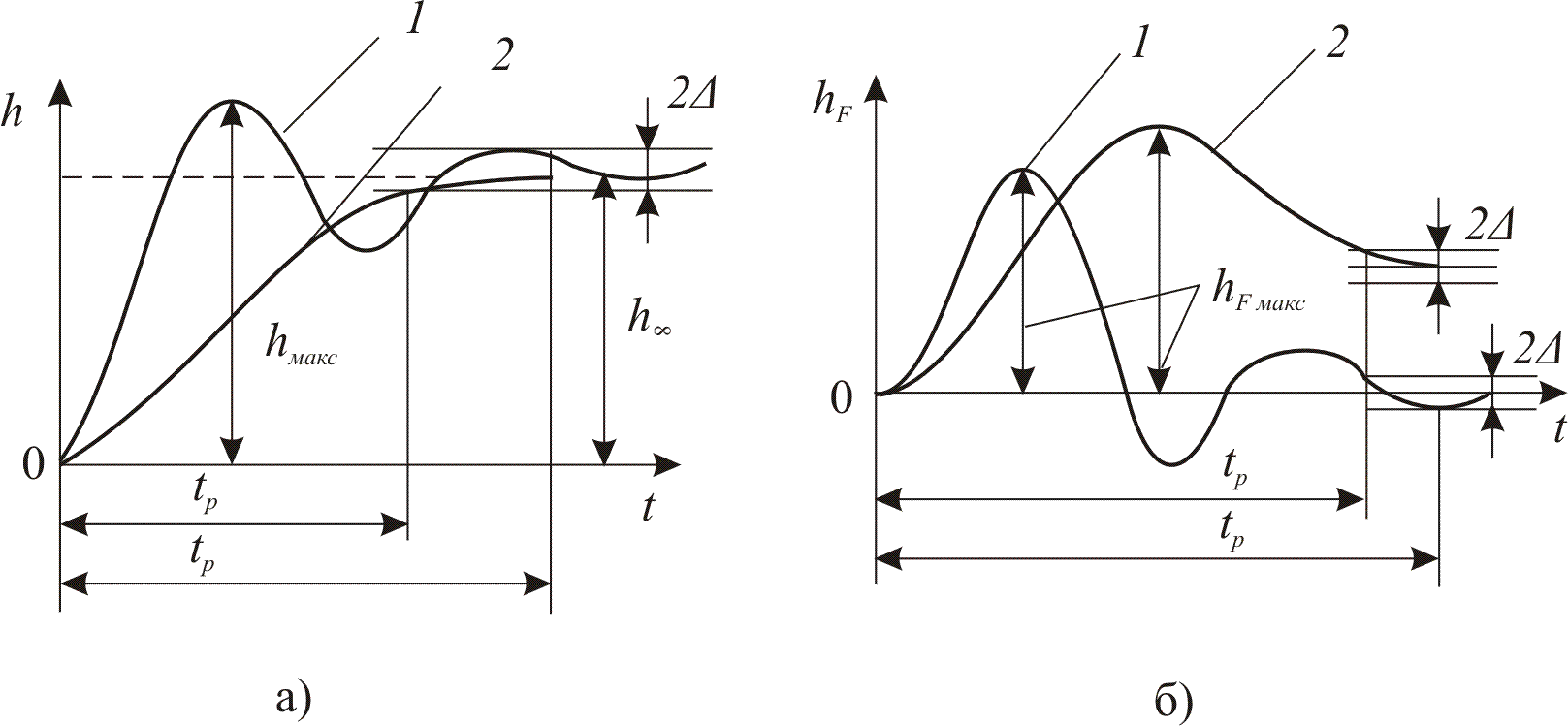
Рис. 9.5. Приклади перехідних характеристик: а - за керуючим впливом; б - за збуренням.

При коливальному затухаючому процесі основними показниками якості є перерегулювання σ, час регулювання і число коливань. Перерегулювання дорівнює різниці між максимальним значенням перехідної характеристики і її усталеним значенням . Перерегулювання, зазвичай, виражають у відносних одиницях:

. /9.20/

Для більшості систем перерегулювання . Час регулювання визначає тривалість перехідного процесу і його приймають рівним інтервалові часу, після закінчення якого відхилення перехідної характеристики від сталого значення не перевищує

. /9.21/

Число коливань дорівнює числу максимумів кривої h(t) за час регулювання. Воно не повиннео перевищувати двох.

Будь-яка система, крім відтворення задаючого впливу, повинна зменшувати вплив збурень. Цю її властивість оцінюють за допомогою перехідної характеристики за збуренням (рис. 9.5,б). Характеристики також можуть мати коливальний затухаючий (крива 1) або монотонний (крива 2) характер.

Параметрами перехідних характеристик є максимальна динамічна похибка і час регулювання . Для визначення часу регулювання відхилення Δ, обчислене за формулою /9.21/, відкладають для астатичних систем від осі абсцис, а для статичних - від статичної похибки .

У кожній системі між перехідними характеристиками h(t) і існує тісний зв'язок: чим швидше встановлюється h(t), тим швидше наближається до усталеної похибки .

Інтегральні оцінки якості

Вони являють собою визначені інтеграли від динамічної похибки і служать відносною мірою тривалості перехідних процесів. Чим менше значення інтегральної оцінки, тим швидше протікає перехідний процес. Найбільш проста інтегральна оцінка

, /9.22/

яка чисельно дорівнює площі, обмеженій кривою .

Інтеграл І₁ обчислюють за допомогою перетворення Лапласа:

. /9.23/

Оцінку І₁ застосовують тільки при монотонних перехідних процесах (рис. 9.6, а). При коливальному затухаючому процесі критерій 1₁ не характеризує швидкодії через алгебраїчне сумування площадок, обмежених кривою і віссю абсцис (рис. 9.6,б). Тому

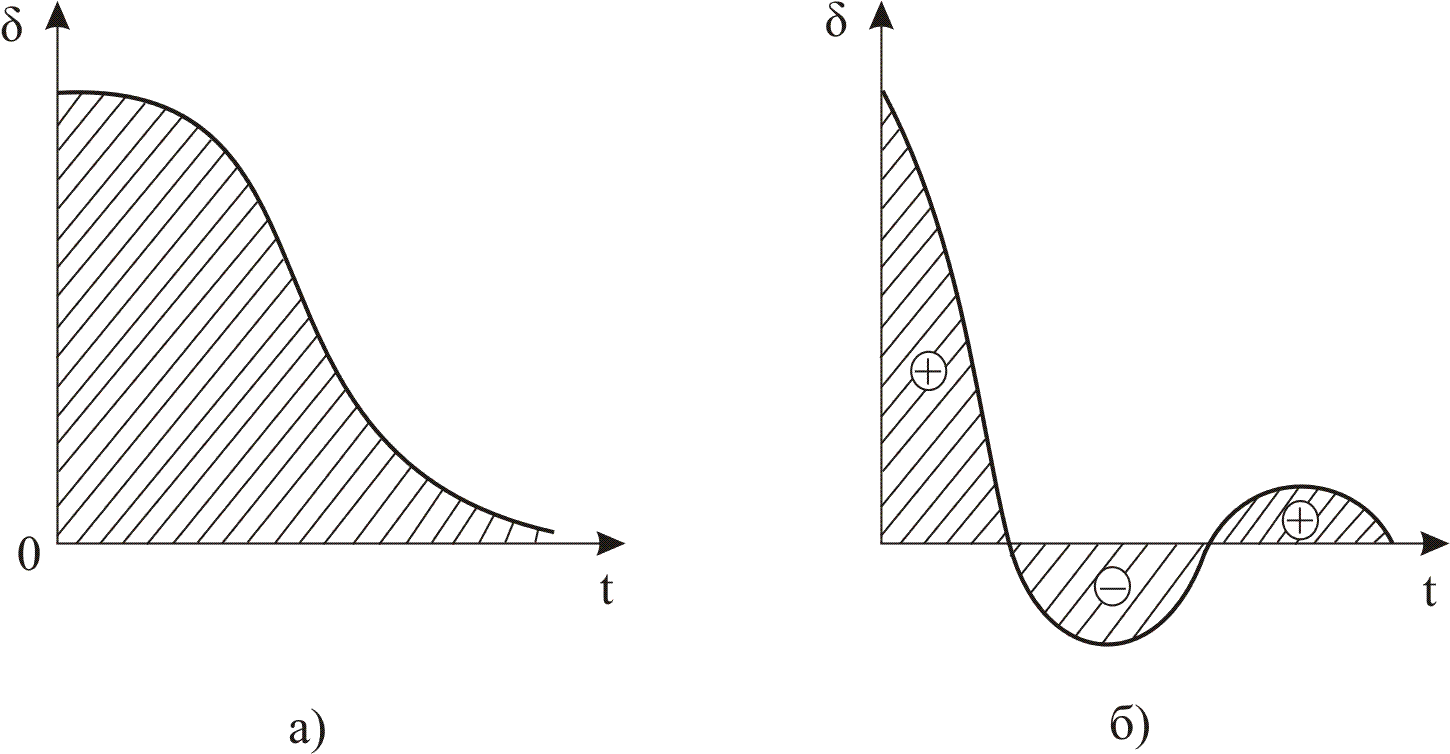
Рис. 9.6. Графічне представлення інтегральної оцінки І₁: а- для монотонного процесу; б - для коливального затухаючого процесу.

для коливально-затухаючих процесів застосовують квадратичну інтегральну оцінку

. /9.24/

Як показано на рис. 9.7, підінтегральна крива розташовується над віссю абсцис і обмежена нею площа може характеризувати швидкодію системи регулювання.

І. М. Макаров і Б. М. Менський приводять формули обчислення для різних видів зображень за Лапласом функцій . За чисельним значенням оцінки І₂ можна судити про час перехідного процесу (час регулювання). Якщо для двох значень якого-небудь параметра, наприклад, коефіцієнта підсилення розімкнутої системи, знайти оцінки , то меншому значенню відповідає менший час регулювання. Тому оцінку І₂ звичайно використовують для знаходження значень варійованих параметрів системи, що доставляють мінімум інтегралу /9.24/.

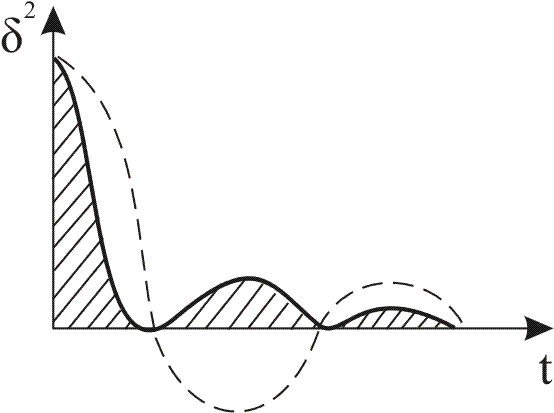
Рис. 9.7. Графічне представлення інтегральної оцінки І₂ для коливально-затухаючого процесу.

Знайдемо, як приклад, значення коефіцієнтів А і В у системі третього порядку з передаточною функцією

,

при яких буде мінімальним.

Якщо , то зображення за Лапласом

. /9.25/

Для /9.25/ згідно /9.24/

. /9.26/

Відшукавши часткові похідні І₂ по А і по В і прирівнюючи їх до нуля, одержимо

,

звідки А=1 і В=2. Знайдені коефіцієнти відповідають коливально-затухаючому перехідному процесові, для якого критерій І₂ мінімальний.

У ряді випадків потрібно, щоб перехідний процес у системі регулювання наближався до бажаного процесу у виді кривої . Визначити параметри системи, які будуть щонайкраще наближати криву до бажаної , можна на основі критерію

. /9.27/

Формули для обчислення підбирають за видом зображення розглянутим вище методом. Потім, мінімізуючи І*, знаходять значення варійованих параметрів.

Оптимальне за швидкодією керування. При проектуванні систем керування часто ставиться задача переведення об'єкта керування з одного стану в інший за мінімальний час при обмеженнях, що накладаються на величину керуючого впливу. До таких об'єктів відносять меліороване поле при підґрунтовому зволоженні і осушенні, ділянку каналу тощо.

Для рішення зазначених задач Л.С. Понтрягін розробив математичну теорію оптимальних процесів (принцип максимуму). Принцип максимуму дозволяє встановити закон зміни керуючого впливу , що забезпечує мінімальний час перехідного процесу.

Застосування оптимальних систем керування до останнього часу стримувалося через складність технічної реалізації функції . Використання мікропроцесорів і комп’ютерів як пристроїв формування дозволяє широко застосувати оптимальні за швидкодією системи керування багатьма меліоративними об'єктами.

Отже, теорія автоматичного регулювання має у своєму розпорядженні великі можливості побудови системи з наперед зданими показниками якості роботи.