Критерій стійкості Найквіста

З частотних критеріїв стійкості найбільше часто застосовують критерій Найквіста, що дозволяє судити про стійкість замкненої системи за видом годографа амплітудно-фазової частотної характеристики розімкненої системи.

Більшість систем автоматичного регулювання складається зі стійких ланок і їх розімкнені системи є стійкими.

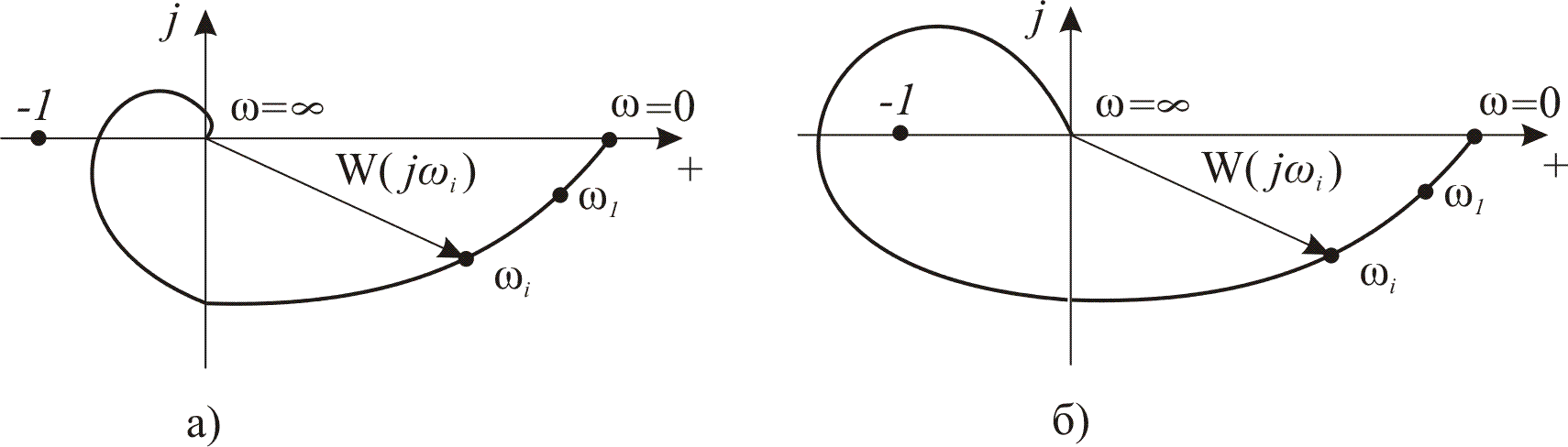
Рис. 9.3. Годографи амплітудно-фазових частотних характеристик стійкої (а) і нестійкої (б) систем.

У цьому випадку для стійкості замкненої системи необхідно і достатньо, щоб годограф амплітудно-фазової частотної характеристики розімкненої системи при зміні частоти від 0 до не охоплював точку з координатами (рис. 9.3, а).

Якщо розімкнена система стійка і годограф охоплює точку з координатами , то замкнена система нестійка (рис. 9.3,б). У випадку, коли годограф проходить через точку , система знаходиться на границі стійкості. Найквіст встановив також критерії стійкості для систем, нестійких у розімкнутому стані, і систем із запізненням.

Застосування частотних критеріїв значно полегшує визначення стійкості тоді, коли замість диференціальних рівнянь окремих елементів відомі їх амплітудно-фазові частотні характеристики. У цьому випадку годограф знаходять графічним шляхом.

Вплив коефіцієнта підсилення на стійкість

Використовуючи розглянуті критерії, легко встановити вплив коефіцієнтів характеристичного рівняння системи на її стійкість. Найбільший практичний інтерес представляє вивчення впливу коефіцієнта підсилення розімкненої системи k на стійкість, тому для зменшення статичної похибки необхідно збільшувати коефіцієнт k. Спростити аналіз можна, розглянувши як приклад систему, яка складається з інерційної і коливальної ланок і відповідає системі регулювання рівня води в басейні, коли поплавок знаходиться безпосередньо в басейні. Рівняння руху такої системи

/9.10/

Характеристичне рівняння

,

де

Підставивши в умову стійкості значення коефіцієнтів, одержуємо

. /9.11/

З нерівності /9.11/ видно, що збільшення коефіцієнта підсилення може призвести до втрати стійкості. Значення коефіцієнта підсилення, при якому система знаходиться на границі стійкості, називається критичним k_кр.

. /9.12/

При k_кр годограф проходить через точку з координатами . У випадку система регулювання стає нестійкою. Тому k_кр визначає граничне значення похибки системи автоматичного регулювання. Отже, між точністю регулювання і стійкістю існує протиріччя. Для його розв’язання, тобто збільшення k_кр, використовують коригувальні ланки.

Ланки, дії яких проявляються тільки в перехідних процесах, називають коригувальними. Такі властивості мають диференціюючи, інтегруючі і інтегрально-диференціюючи ланки.

Якщо, наприклад, інерційну ланку з передаточною функцією охопити диференціюючою ланкою з передаточною функцією , то передаточна функція з'єднання

. /9.13/

Як видно з /9.13/, охоплення інерційної ланки диференціюючою призводить тільки до збільшення сталої часу, а коефіцієнт підсилення з'єднання не змінюється. Тому при заданому значенні коефіцієнта підсилення системи k стійкість можна забезпечити за рахунок відповідного вибору коефіцієнта k ₂.

У гідравлічних системах регулювання як коригувальний пристрій використовують ізодроми різного конструктивного виконання.

Якість процесів регулювання

Стійкість - це необхідна, але недостатня умова працездатності систем автоматичного регулювання. Кожна система повинна забезпечувати також задану точність в усталених режимах і бажаний вид перехідних процесів. Дані вимоги до систем і визначають якість процесів регулювання.

Точність в усталених режимах

У загальному випадку точність регулювання в усталеному режимі визначається двома складовими:

, /9.14/

де х_в - точність відтворення задаючого впливу; - точність компенсації збурення.

Формули для обчислення х_в і досить просто знайти за відомими передаточними функціями замкнених систем. Дійсно, в усталеному режимі всі похідні в диференціальному рівнянні дорівнюють нулю. Тому, підставивши у вирази передаточних функцій Ф(р) і Ф_F(р) р=0, одержують рівняння усталених режимів.

При сталому вхідному впливові х₀

. /9.15/

Аналогічно при сталому збуренні F₀

. /9.16/

Вид рівнянь Ф(0) і Ф_F(0) залежить від наявності інтегруючих ланок в одноконтурній системі регулювання. Коли система не містить інтегруючих ланок, то передаточна функція розімкненої системи з одиничним зворотнім зв’язком W(0)=k і . Така система відтворює вхідний сигнал з похибкою, тому її називають статичною системою.

Якщо одноконтурна система містить хоча б одну інтегруючу ланку, то W(0)=0, Ф_F(0) = 0 і система відтворює вхідний сигнал без похибки. Система, що володіє такою властивістю, називається астатичною системою. Похибка тут також дорівнює нулеві.

Похибка, викликана дією збурення у статичній системі,

, /9.17/

де - коефіцієнт підсилення всіх ланок, що знаходяться між точкою прикладання збурення і регульованою величиною.

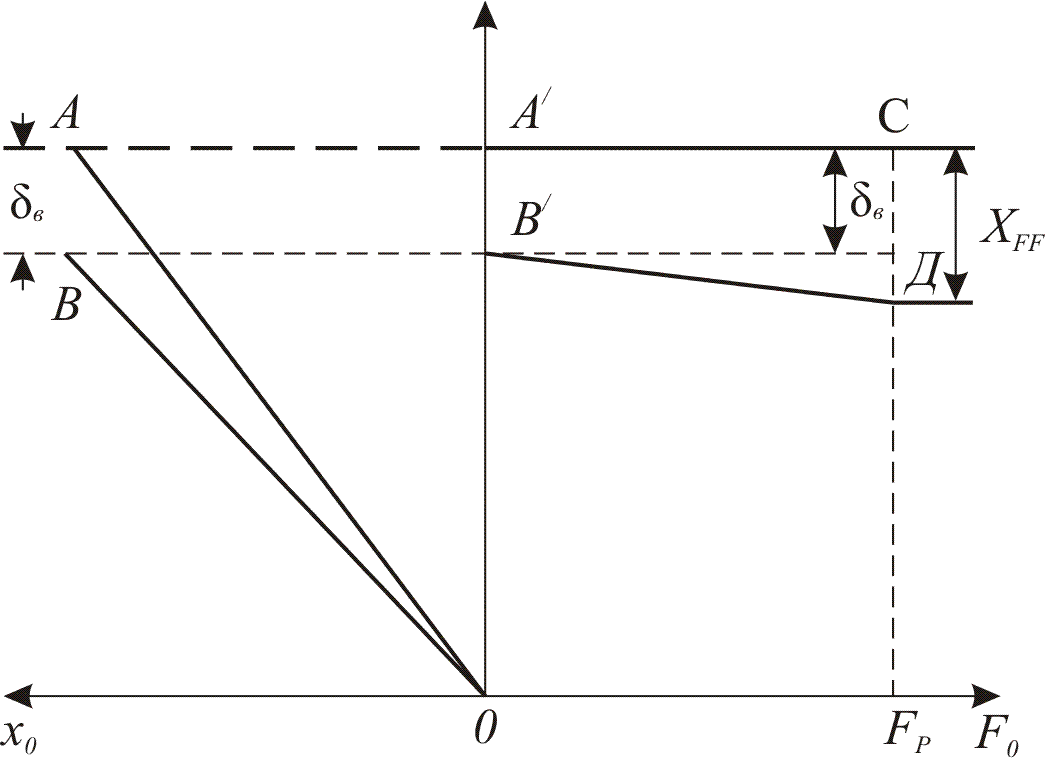
Рис. 9.4. Статичні характеристики астатичної (АО і А'С) і статичної (ВО і В'Д) систем.

Отже, в астатичній системі , а в статичній –

. /9.18/

Як видно з рівняння статичної характеристики /9.18/, точність роботи системи тим вище, чим більше коефіцієнт підсилення розімкненої системи. Прикладом статичної системи є система стабілізації рівня води в басейні.

На рис. 9.4 показані характеристики астатичної і статичної систем автоматичного регулювання.

Характеристика астатичної системи відповідає рівнянню і є бісектрисою прямого кута (пряма ОА); в статичній системі має місце похибка , тому її характеристика зображується прямою ОВ, що лежить нижче прямій ОА. Отже, в статичній системі вхідний сигнал повинний бути на більшим вхідного сигналу в астатичній системі для одержання рівних значень регульованих величин.

В астатичній системі регульована величина не залежить від збурення (рис.9.4, пряма А'С), тому що . У статичній системі зі збільшенням збурення F похибка зростає (пряма В'Д). Значення похибки при розрахунковому значенні збурення F_p визначає клас точності системи. Якщо задана похибка в одиницях регульованої величини, то з /9.17/ розрахунковий коефіцієнт підсилення розімкненої системи

. /9.19/

Похибки і прийнято називати статичними показниками якості роботи систем автоматичного регулювання.