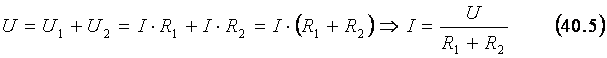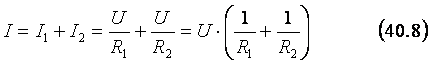Вывод из уравнений Максвелла[править | править исходный текст]

Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)

где   — плотность тока в пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системеСГС):

Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:

Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:

Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:

Тогда магнитное поле определяется интегралом (в системе СГС)

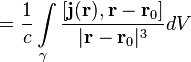
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что

получим закон Био — Савара — Лапласа для поля витка с током.

Применение[править | править исходный текст]

Пусть требуется найти модуль магнитной индукции в центре очень тонкой (все витки уложены вблизи одной окружности) катушки с числом витков  , по которой течет ток  . Найдём магнитную индукцию, создаваемую одним витком катушки. Из формулы

получим модуль магнитной индукции как

где   — радиус катушки (в данном случае — константа),   — угол между вектором   (радиус-вектором из центра витка к элементу витка) и   (элементом витка) — равен  .

Проинтегрировав обе части, получаем

где   — сумма длин всех элементов проводника витка, в данном случае — длина окружности, тогда

Так как в катушке содержится   витков, то суммарный модуль магнитной индукции равен

13. Закон Ампера для циркуляції магнітного поля — твердження про те, що інтеграл по замкненому контуру від магнітної індукції пропорційний силі електричному струму, що протікає через площу, обмежену контуром. Закон сформулював у 1826 році Андре-Марі Ампер. У модифікованому вигляді він входить до основних рівнянь електродинаміки.

Наслідком закону Ампера є те, що струми, які протікають за межами контура, не дають внеску в циркуляцію.

Зміст

  [сховати] 

• 1 Формулювання

  • 1.1 Інтегральна форма

  • 1.2 Диференційна форма

• 2 Модифікація з врахуванням змінного електричного поля

• 3 У середовищі

• 4 Джерела

Формулювання[ред. • ред. код]

Інтегральна форма[ред. • ред. код]

У системі одиниць СГС закон Ампера має вигляд:

,

де   — магнітна індукція,   — густина струму,   - швидкість світла.

У СІ :

,

де   — магнітна стала.

Закон справедливий для постійних струмів і полів. У разі змінних струмів в формулі з'являється член, пов'язаний із струмом зміщення.

Диференційна форма[ред. • ред. код]

В диференційній формі закон Ампера набирає вигляду (СГС):

або (СІ)

Модифікація з врахуванням змінного електричного поля[ред. • ред. код]

Змінне електричне поле є додатковим джерелом, що породжує магнітне поле. З його врахуванням закон Ампера змінює форму. Для вакууму він набирає вигляду (СГС):

,

де   — напруженість електричного поля. Величину

де   - вектор електричної індукції, називають струмом зміщення. Для вакууму  .

У середовищі[ред. • ред. код]

Закон Ампера для циркуляції магнітного поля можна використовувати також і для середовища, однак при цьому потрібно враховувати всі струми, які виникають у середовищі. Це не тільки струми вільних зарядів, а струми зарядів, зв'язаних в складі атомів і молекул. Такі струми виникають з двох причин. По-перше, зв'язані електрони в магнітному полі прецесують, створюючи струм намаганіченння, по-друге, у випадку змінного електричного поля, електрони зміщуються відносно йонів, з якими вони зв'язані, створюючи струм поляризації. Враховуючи всі ці струми закон Ампера для середовища, записують в такій формі, щоб у ньому залишилися тільки струми вільних заряджених частинок:

,

де   - напруженість магнітного поля,   — струм вільних зарядів. При цьому внесок струмів намагнічування входить у визначення  , а внесок струмів поляризації — у визначення  .

У диференційній формі закон Ампера набирає вигляду (СГС):

7. Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрическогопроисхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работеэтих сил по перемещению единичного положительного заряда вдоль всего контура^[1].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил  , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре   ЭДС будет равна:

где   — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого́ источника равна нулю.

ЗАКОН ОМА. СОПРОТИВЛЕНИЕ ПРОВОДНИКА. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ.

Закон Ома помогает определить силу тока через проводник, давая возможность оценить тепловое, химическое и магнитное действие электрического тока.

Для существования постоянного тока в проводнике необходимо поддерживать неизменной разность потенциалов между его концами. С ростом этой разности потенциалов напряжённость поля в проводнике увеличивается, и свободные заряды проводника приобретают бóльшую скорость, а значит, растёт сила тока через проводник. Немецкий физик Г. Ом установил, что сила тока I через металлический проводник прямо пропорциональна напряжению U между его концами:

где R – постоянная величина, называемая сопротивлением данного проводника (рис. 40а). Уравнение (40.1) называют законом Ома для участка цепи, который также оказался справедлив и для электролитов. Единицей сопротивления в СИ является Ом. Согласно (40.1) проводник имеет сопротивление 1 Ом, если при напряжении 1 В между его концами через него течёт ток 1 А.

Работа вольтметра – прибора для измерения напряжения, основана на законе Ома. Вольтметр (см. V на рис. 40б), как и амперметр, измеряет ток, проходящий через него. Зная сопротивление вольтметра R и силу тока I, по закону Ома определяют напряжение U между точками, к которым подключён вольтметр. Вольтметр градуируют так, чтобы он показывал напряжение в вольтах, а не ток, который через него проходит.

Сопротивление зависит от материала, из которого сделан проводник, и его размеров. Для проводника с постоянной площадью поперечного сечения S (рис. 40в) справедливо следующее соотношение между его длиной l и сопротивлением R:

где  - постоянный коэффициент, называемый удельным сопротивлением проводника и зависящий от вещества, из которого сделан проводник. Единицей удельного сопротивления является Ом^.м. Удельное сопротивление металлов гораздо меньше, чем у диэлектриков. Так, удельное сопротивление меди и алюминия составляет 1,7^.10^-8 и 2,8^.10^-8 Ом^.м, а у фарфора и сухого дерева оно достигает 10¹³ и 10⁸ Ом^.м, соответственно.

Ток течёт по проводникам, образующих электрическую цепь. Соединение проводников 1 и 2, показанное на рис. 40г, называют последовательным. Очевидно, что сила тока в обоих проводниках одинакова:

I₁ = I₂ = I         .                          (40.3)

Работа по перемещению заряда из А и В на рис. 40г равна сумме работ по его перемещению из А в Б и из Б в В, а значит,

              U = U₁ + U₂    ,                           (40.4)

где U – напряжение между точками А и В. Если R₁ и R₂ –сопротивления проводников 1 и 2, то уравнение (40.4) можно переписать в следующем виде, учитывая (40.1) и (40.3):

Из сравнения (40.5) и (40.1) следует, что сопротивление R двух последовательно соединённых проводников равно:

R = R₁ + R₂      .                          (40.6)

Параллельное соединение проводников показано на рис. 40д. Очевидно, что сила тока I через участок цепи АБ равна:

I = I₁ + I₂         .                          (40.7)

Учитывая (40.1), можно переписать уравнение (40.7) как:

Из сравнения (40.8) и (40.1) следует, что для сопротивления R двух параллельно соединённых проводников справедливо:

Уравнения, аналогичные (40.6) и (40.9) можно применять для любого числа последовательно и параллельно соединённых проводников, соответственно.

Вопросы для повторения:

        Как формулируется закон Ома для участка цепи?

        Что такое сопротивление, и в каких единицах его измеряют?

        Как работает вольтметр?

        Чему равно сопротивление цилиндрического проводника?

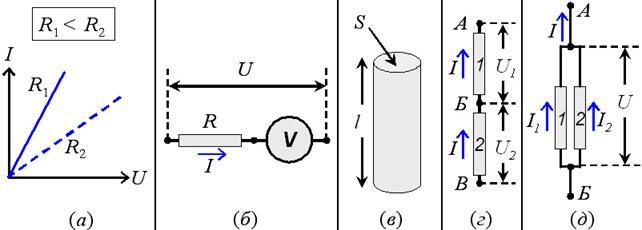
Рис. 40. (а) – иллюстрация закона Ома для проводников с сопротивлением R₁ и R₂; (б) – к объяснению работы вольтметра; (в) – к объяснению формулы (40.2); (г,д) - последовательное и параллельное соединение проводников, соответственно.