26. Алгоритм решения задачи лп с двумя переменными графическим методом.
1) Строится область допустимых решений (ОДР).
2) Если ОДР является не пустым множеством, то строится вектор
n (с₁,с₂), выходящий из начала координат.
3) Перпендикулярно вектору n проводится одна из линий уровня, например: линия уровня, соответствующая уровню с₁х₁ + с₂х₂ = 0
4) Линия уровня перемещается параллельно самой себе в направлении вектора n.
5) Перемещения линии уровня происходит до тех пор, пока у неё не окажется только одна общая точка с ОДР. Эта точка определяет единственное решение задачи и является точкой экстремизма.
6) Находим координаты точки экстремизма и значение целевой функции в ней.
27. Особые случаи при решении задачи лп.
1) Неединственность решения.
2) Отсутствие оптимального плана в силу неограниченности целевой функции.
3) Отсутствие оптимального плана в силу противоречивости ограничений.
Особый случай 1: связан с недостаточностью числа критериев
(целевых функций).
2: связан с недостаточностью числа ограничений.
3: связан с избытком ограничений.
28. Понятие оценки опорного плана. Необходимые и достаточные условия оптимальности. Симплексный метод.
Существует универсальный способ решения ЗЛП называемый симплекс-методом.
Симплекс-метод является основным в решении задач линейного программирования.
Симплекс-метод является универсальным и может быть применен к любой задаче линейного программирования записанной в канонической форме.
В этом случае системой ограничений выступает система линейных уравнений, причем в этой системе количество переменных больше количества уравнений.
Базисные решения называются допустимыми или опорными решениями если в нем значения переменных не отрицательны.
Симплекс метод вносит определённый порядок при нахождении, как базисного решения так и при переходе к последующим решениям.
Если 1-же решение оказалось допустимым, то его проверяют на оптимальность. Если оно не оптимально, то производится переход к следующему.
29. Симплексные таблицы. Алгоритм симплексного метода.
Симплекс- таблицы являются компактной записью задачи линейного программирования. Перед составлением симплекс-таблицы, задача должна быть представлена в виде
системы уравнений записанной в допустимом виде.
Алгоритм симплексного метода:
Определить число и состав базисных и свободных переменных.
Выразить базисные переменные через свободные переменные.
Выразить целевую функцию через свободные переменные.
Построить начальную симплекс-таблицу.
Проверить решение на оптимальность.
Проверить существование решения.
Пересчитать симплекс-таблицу.
После заполнения новой симплекс-таблицы алгоритм возвращается к проверке решения на оптимальность.
30. Симплекс-метод решения задачи с начальным базисом.
Для его решения ЗЛП должна содержать единичную подматрицу размером m(на)m – в этом случае очевиден начальный опорный план.
Проверка оптимальности опорного плана происходит с помощью оптимальности. Переход к другому опорному плану проводится с помощью преобразований Гаусса. Полученный опорный план снова проверяется на оптимальность и т.д.
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс разности.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Аr, который даёт минимальное положительное оценочное отношение.
Строка Аr называется направляющей, столбец Ак и элемент аrк-направляющим.
Элементы направляющей строки в новой симплекс-таблице вычисляется по формулам:
=
/
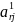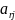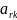
а
элементы i-ой
строки, по формуле:
=(
*
-
*
)/
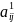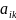Значения нового опорного плана рассчитываются по формулам:
=
/
=(
*
-
*
)
/
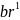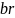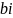Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности целевой функции.
Если среди симплекс-разностей оптимального плана нулевые только оценки, соответствующие базисным векторам, то это значит что оптимальный план единственен. Если же нулевая оценка соответствует вектору, не входящему, то это означает, что оптимальный план не единственный.