Вопрос №47 Производные и дифференциалы высших порядков

Дифференциалом второго порядка функции y = f(x) называется дифференциал от дифференциала первого порядка.

d²y= d(dy)

Диф. 2-го порядка называется дифференциал от дифференциала первого порядка.

d²y = d(d^n-1y)

d²y = d(f`(x))`d(x) = d*(f`(x))`dx = (f`(x))`dxdx = f``(x)dx²

Вторая производная – это производная от первой производной:

f``(x) =

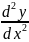
Если функция n раз дифференцируема на каком либо промежутке Х то можно записать:

F(x) принадл. D⁽ⁿ⁾ (x)

Вопрос №48 Теорема Ферма

Теорема: Если дифференцируемая на промежутке Х функция y = f(x) достигает своего наименьшего или наибольшего значения в точке х₀, то производная функция этой точки = 0.

Д

Δy = f(x₀+Δx) – f(x₀) ≥ 0 =>

≥ 0 (x>0) или

≤ 0 (x<0)

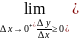
Т.к. функция дифференцируема на промежутке Х то значение производной не зависит от направления:

=

f`(x₀) = 0

ок-во:

y

f(x₀+Δx)

Х

0 Х₀ х₀+Δх

Вопрос №49 Теорема Коши. Правило Лопиталя (без док-ва)

Теорема: Пусть функция y = f(x) удовлетворяет след.условиям:

• f(x) принадл. C[a;b]

• f(x) принадл. D`(a;b)

а так же существует функция g(x), которой удовлетвор. тем же условиям, а так же её производная ≠0 . тогда существует точка £ из промежутка (a;b) такая, что:

Док-во: F(x) = f(x) - 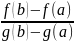(g(x) – g(a))

Проверим, выполняются ли условия для новой функции:

1. F(x) непрерывна на отрезке [a;b] по 1-му условию данной теоремы;

2. F(x) принадл. D`(a;b) по 2-му условию

3. F(a) = ( g(a) – g(a) )

F(a) = f(a)

F(b) = f(b) = 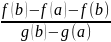( g(b) – g(b))

F(b) = f(a)

По теореме Ролля найдем хотя бы 1 точку, где F`(x) = 0:

F`(£) = 0

F`(x) = f`(x) =

F`(£) =

F`( =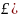

Поделив обе части на нулевую производную g в точке £ получаем доказываемое равенство.

Правило Лопиталя:

Предел отношения двух бмв или ббв равно приделу отношения их производных, если последний существует:

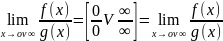
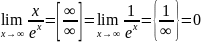
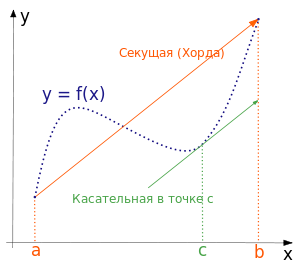
Вопрос №50 Теорема Лагранжа. Формула конечных приращений

Теорема Лагранжа:

Пусть функция y = f(x) удовлетворяет условиям:

• f(x) принадл. C[a;b]

• f(x) принадл. D`(a;b)

тогда найдется хотя бы одна точка £ принадл. (a;b) такая что:

f`(£) =

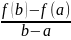
Найдется хотя бы 1 точка, в которой касательная, проведенная к графику будет || к хорде , проведенная от начальной к конечной точке на этом промежутке.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция   непрерывна на отрезке   и дифференцируема в интервале  , то найдётся такая точка  , что

.

Геометрически это можно переформулировать так: на отрезке   найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Вопрос №51

Возрастание и убывание ф-ии. Признак монотонности ф-ии

Признак монотонности функций

Теорема 1. Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна). Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает). 

Вопрос №52

Дифференцируемые ф-ии одной переменной. Условие постоянства ф-ии в области

Функция   одной переменной является дифференцируемой в точке   своей области определения  , если существует такая константа  , что для любой точки   верно

при этом число   неизбежно равно производной

Функция одной переменной является дифференцируемой в точке   тогда и только тогда, когда она имеет производную в этой точке.

Условие постоянствa функции

Пусть производная функции равна нулю на некотором промежутке. Тогда эта функция постоянна на этом промежутке.  Теорема обобщается на случай функции нескольких переменных. Если все частные производные функции тождественно равны нулю в некоторой области, на которой определена эта функция, она постоянна в этой области.