Вопрос №38 Непрерывность числовой ф-ии одной переменной в точке. Точки разрыва, классификация точек разрыва

Функция y=f(x) называется непрерывной в точке x0 ,если существует предел функции в этой точке и он равен значению функции в этой точке.

Точки разрыва функции

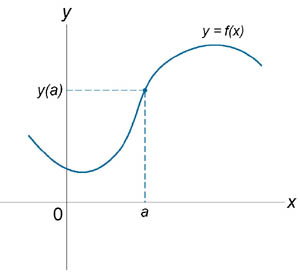
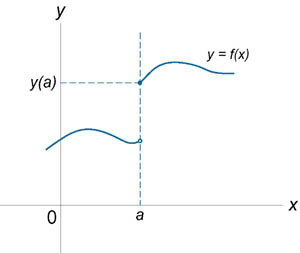
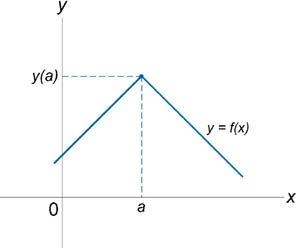
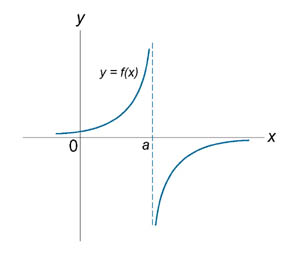
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв Непрерывна при x = a. Имеет разрыв при x = a. Непрерывна при x = a. Имеет разрыв при x = a. Рисунок 1. Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке Существуют левосторонний предел   и правосторонний предел  ; Эти односторонние пределы конечны. При этом возможно следующие два случая: Левосторонний предел и правосторонний предел равны друг другу: Такая точка называется точкой устранимого разрыва. Левосторонний предел и правосторонний предел не равны друг другу: Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции. Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Вопрос №39

Непрерывность ф-ии на отрезке. Теоремы Коши о непрерывных функциях (без доказательства)

Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

Теорема Коши:если функция y=f(x) непрерывна на отрезке [a;b] и принимает на его концах неравные значения f(a)=A и f(b)=B,то на этом отрезке она принимает и все промежуточные значения между A и B.

Вопрос №40

Производная функции в точке. Геометрическая интерпретация производной

Производной функцией называют предел, отношение прирощения функции к прирощению аргумента при условии, что последнее → 0

Геом.смысл: Значение производной в точке равно tg угла наклона касательной, проведенной к функции в этой точке

Вопрос №41

Производная функции в точке. Механическая интерпретация производной

Производной функцией называют предел, отношение прирощения функции к прирощению аргумента при условии, что последнее → 0

Механический смысл:

Пусть некоторая точка движется вдоль прямой не обязательно с постоянной скоростью. Тогда пройденное расстояние измеряется по закону S = S(t)

Необходимо вычислить скорость в момент времени t₀

V(t₀) - ?

V_ср =

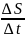
Естественно полагать, что предельной формой V_ср при Δt→0 является скорость в момент времени t₀

V(t₀) = 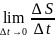= S`(t₀)

Механический смысл производной – производная от закона S(t) = S

Вопрос №42

Производная функции в точке. Эластичность ф-ии

Производной функцией называют предел, отношение прирощения функции к прирощению аргумента при условии, что последнее → 0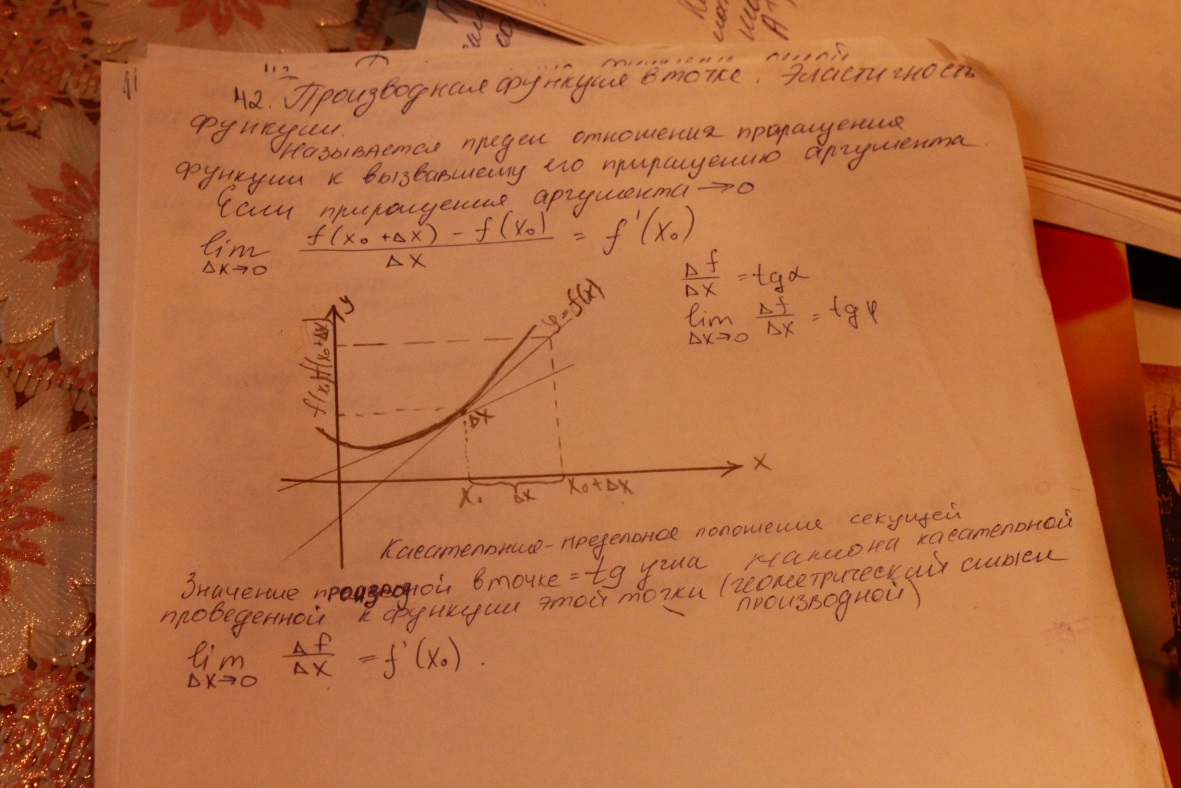

Вопрос №43

Дифференцируемые функции одной переменной. Необходимое и достаточное условие дифференцируемости

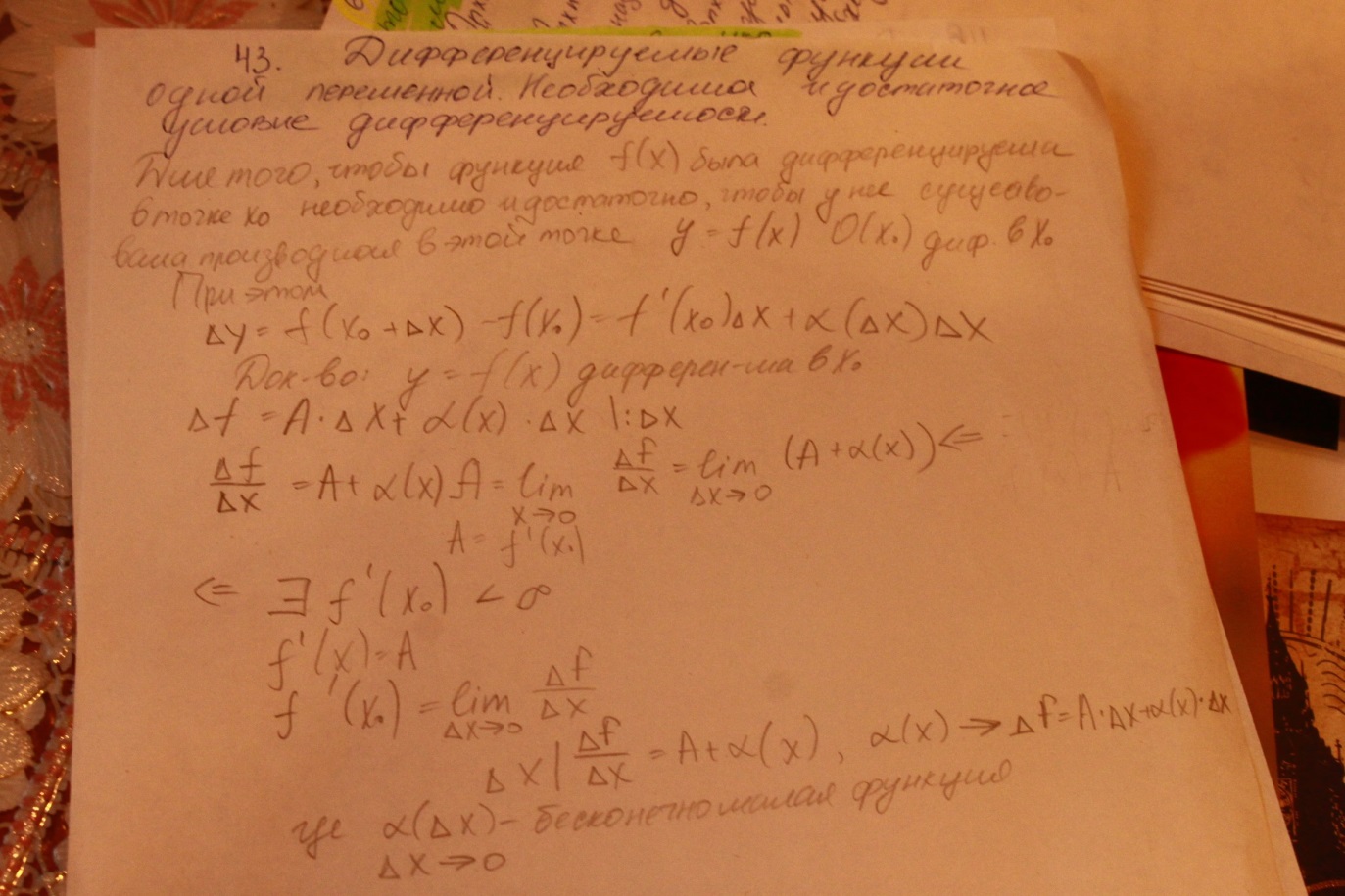
Вопрос №44

Дифференцируемые функции одной переменной. Дифференциал функции одной переменной. Непрерывность дифференцируемой ф-ии

Вопрос №45

Производная ф-ии в точке. Правила дифференцирования

Производной функцией называют предел, отношение прирощения функции к прирощению аргумента при условии, что последнее → 0.

Правила дифференцирования:

1. (С * U(x))` = C*U`(x)

2. (U(x) ± V(x))` = U`(x) ± V`(x)

3. (U(x) * V(x))` = U`(x)*V(x) + U(x)*V`(x)

(U(x) / V(x))` =

Вопрос №46

Производная ф-ии в точке. Дифференцирование сложной функции

Производной функцией называют предел, отношение прирощения функции к прирощению аргумента при условии, что последнее → 0.

Пусть  функция x = f(t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f(t). Тогда сложная функция y = f(f(t)) дифференцируема в точке t, причем справедлива формула

(f(f(t)))' = f'(x)f'(t).

(3)

Доказательство. Зададим x = f(t) отличное от нуля приращение D t. Этому приращению отвечает приращение D x = f (t+D t)-f (t) функции x = f(t). ПриращениюD x отвечает приращение D y = f(x+ D x)-f(x). Так как функция y = f(x)дифференцируема, то ее приращение D y представимо в виде (1):

D y =f'(x)D x +a (D x) D x,

где lim_D x® 0a (D x ) = 0. Поделив данное выражение на D t № 0, будем иметь:

D y/D t=f'(x)D x/D t+ a (D x)D x/D t.

Из дифференцируемости функции x = f (t) в точке t вытекает, что

lim_D t® 0D x/D t = f'(t).

Отметим, что из дифференцируемости функции x = f(t) следует, что D x® 0 при Dt® 0. Следовательно, lim_D t® 0a (D x) =0. Таким образом, получим необходимую формулу (3).