Вопрос №16 Скалярное произведение векторов. Свойства скалярного произведения. Угол между векторами
Скалярным произведением векторов «а» и «в» называется число, равное произведению длин этих векторов на косинус угла между ними.
а*в = |а| * |в| * cosФ - угол между векторами «а» и «в»
Свойства:
а*в = в*а – свойство коммуникативности
р
авенство
0 скалярного произведения свидетельствует
о перпендикулярности этих векторов, и
наоборот. а*в = 0 а
вДля любого вектора «а» произведение на самого себя = вектор «а»2
а(в+с) = а*в + а*с
(λ*а)в = λ(а*в)
Для вычисления cos угла между векторами:
x*y=|x| * |y| cosФ
cosФ
=
Вопрос №17 Скалярное произведение векторов. Необходимое и достаточное условие ортогональности векторов
Скалярным произведением векторов «а» и «в» называется число, равное произведению длин этих векторов на косинус угла между ними.
а*в = |а| * |в| * cosФ - угол между векторами «а» и «в»
Необходимое и дост усл:
Для перпендикулярности
двух ненулевых векторов 
и 
необходимо
и достаточно, чтобы их скалярное
произведение равнялось нулю, то есть,
чтобы выполнялось равенство 
.
Доказательство.
Пусть
векторы
и
перпендикулярны.
Докажем выполнение равенства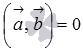 
.
По определению скалярное
произведение векторов равно
произведению их длин на косинус угла
между ними. Так как векторы
и
перпендикулярны,
то угол между ними равен девяноста
градусам, следовательно,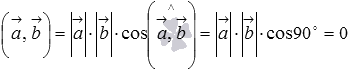 
,
что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что . Докажем, что векторы и перпендикулярны.
Так как векторы
и
ненулевые,
то из равенства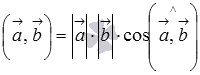 
следует,
что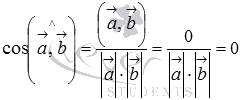 
.
Таким образом, косинус угла между
векторами
и
равен
нулю, следовательно, угол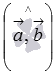 
равен 
,
что указывает на перпендикулярность
векторов
и
.
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Вопрос №18
Скалярное произведение векторов в ортнонормированном пространстве. Длина вектора
Скалярным произведением векторов в ортонормированном базисе равно сумме попарных произведений соответствующих координат
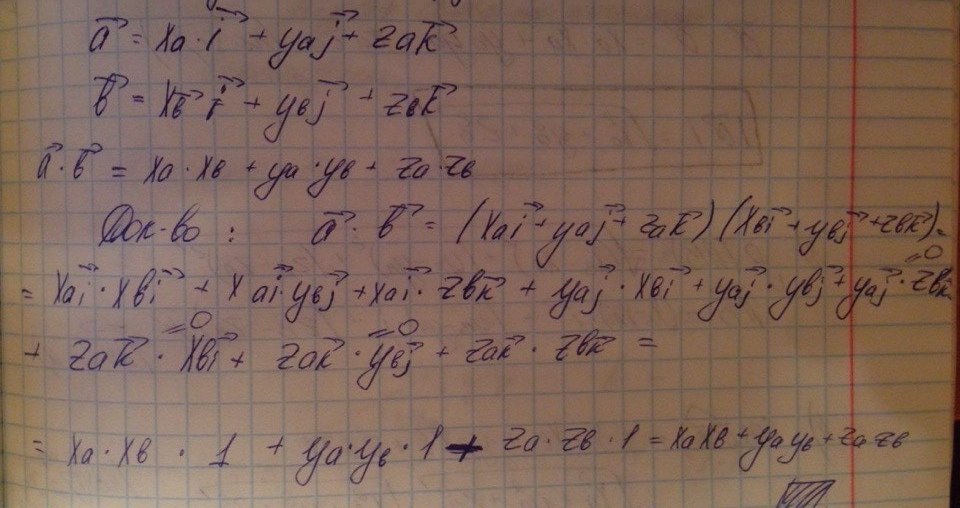
Длина вектора – это расстояние между точками а и b.
Вопрос №19
Прямая на плоскости. Взаимное расположение прямых на плоскости
Две прямые на плоскости могут совпадать.
Две прямые на плоскости могут пересекаться (Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными)
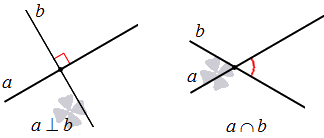
Две прямые на плоскости могут быть параллельными. (Две прямые на плоскости называются параллельными, если они не имеют общих точек)
Вопрос №20
Прямая в пространстве. Взаимное расположение прямых в пространстве
Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).
Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку.
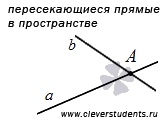
В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек.
Вопрос №21
Плоскость. Взаимное расположение плоскостей
Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.
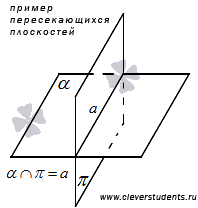
Две плоскости в пространстве могут пересекаться.
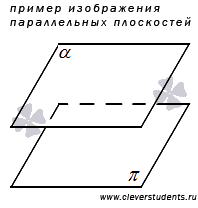
Две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек.
Вопрос №22
Взаимное расположение прямой и плоскости в пространстве
Прямая и плоскость в пространство могут:
а) не иметь общих точек;
б) иметь ровно одну общую точку;
в) иметь хотя бы две общие точки.
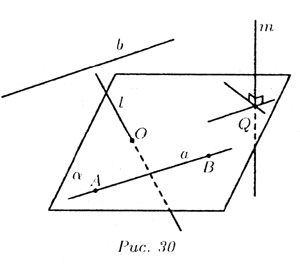
На рис. 30 изображены все эти возможности.
В случае а) прямая b
параллельна плоскости
:
b ||
.
В случае б) прямая l
пересекает плоскость
в
одной точке О; l 
=
О.
В случае в) прямая а
принадлежит плоскости
:
а
или а 
.
Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости , то прямая параллельна плоскости .
Вопрос №23
Способы задания множества. Множество и подмножество. Объединение множеств и его свойства
Множество А называют подмножеством В, если любой элемент А принадлежит В.
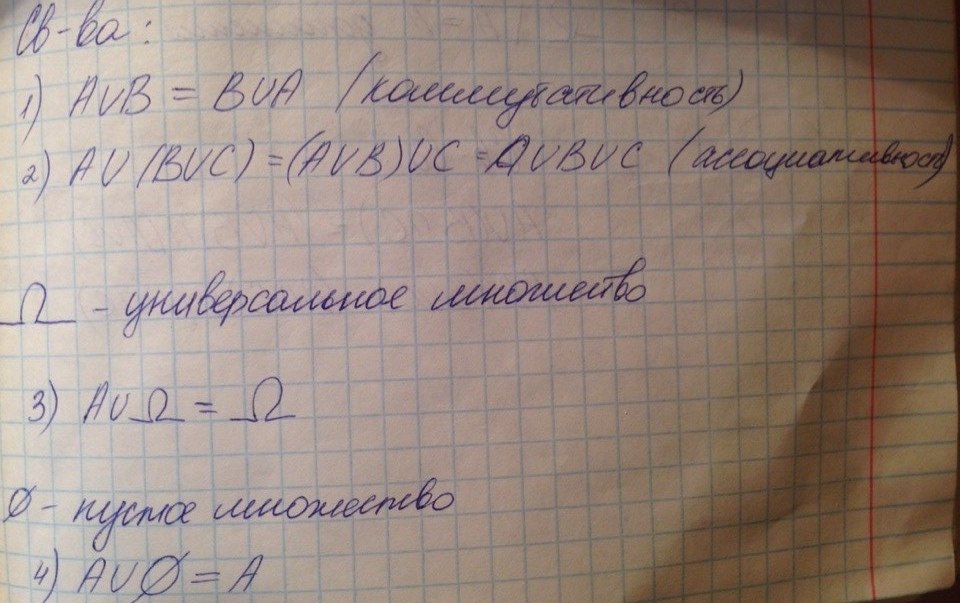
Вопрос №24
Множество. Пересечение множеств и его свойства. Числовые множества
Множеством элементов называется совокупность, отличающаяся друг от друга, но с другой стороны отличающихся от всех остальных элементов
Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B.
Множество А называют подмножеством В, если любой элемент А принадлежит В.
Вопрос №25
Множества на числовой прямой. Окрестность тоски, б – окрестность точки, окрестность бесконечно удаленной точки
Вопрос №26
Предел функции одной переменной. Графическое представление
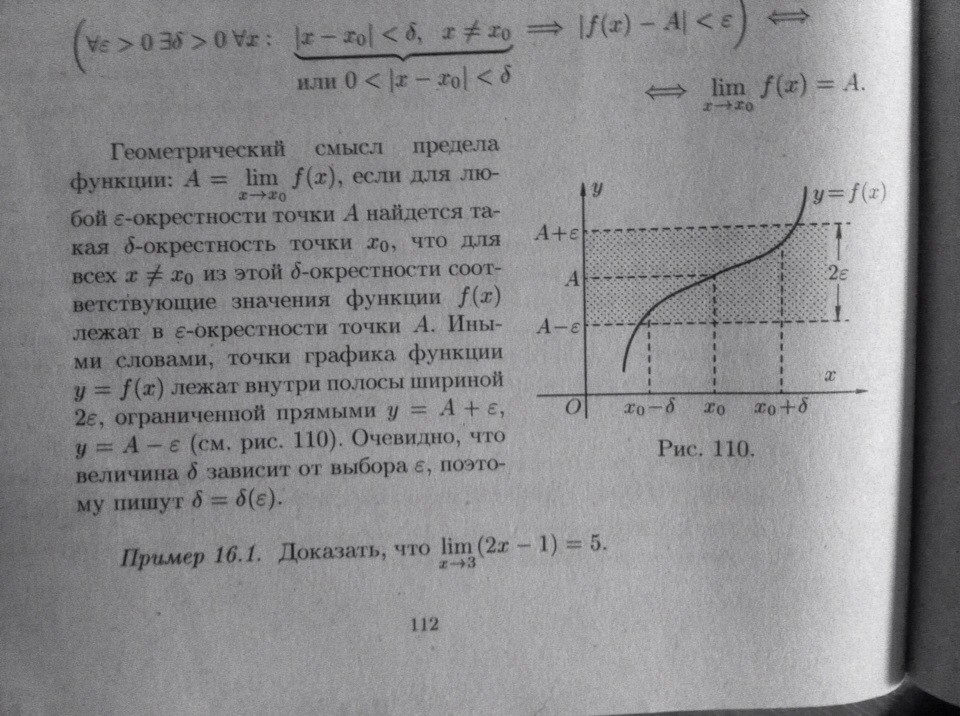
Вопрос №27
Теорема об арифметических действиях над функциями, имеющими конечный предел
Пусть есть 2 ф-ции, имеющие конечн. предел в точке Х0, тогда предел суммы равен сумме пределов, множитель (константу) можно выносить за знак предела, предел произведения = произведению пределов, предел частного равен = частному пределов, если в знаменателе не 0.
Вопрос №28
Предел функции одной переменной. Теорема о единственности предела
Функция не может иметь в одной точке два различных предела.
Вопрос №29
Предел функции одной переменной. Теорема о сжатой переменной
f(x)
, g(x)
, φ(x)
Ǝ O(Xo)
:
x
O(Xo)
f(x)
≤ g(x) ≤ φ(x)
=
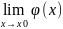= A , A < ∞ => Ǝ
= A
Если функции по бокам имеют одинаковый предел, то функция в середине имеет такой же предел.
Доказательство: = A , A < ∞
∀
ℇ >
0 Ǝ
> 0 ∀
x
∈ X
: 0 < | X
– Xo|
< δ
| f(x) – A | < ℇ преобразуем - ℇ < f(x) – A < ℇ
= A , A< ∞
∀ ℇ > 0 Ǝ ´ > 0 : ∀ x ∈ X : 0 < | X – Xo| < ´
| φ(x) – A | < ℇ преобразуем -ℇ < φ(x) – A < ℇ Получилось 2 дельта окрестность одной точки
Для
всякого ℇ > 0 нашлась такая O
(
∀ x
∈ X
: 0 < | X
– Xo|
<
-ℇ < g(x) < ℇ => -ℇ < f(x) – A < ℇ => | g(x) – A | < ℇ , что и т.д.
Вопрос №30
Предел функции одной переменной. Теорема о предельном переходе в неравенстве
= A , A< ∞
= B
Ǝ O (Xo) ; ∀ x ∈ O (Xo) f(x) < g(x) => A< B
Доказательство: Пусть f(x) < g(x) , A>B (от противного)
Рассмотрим
=
A
- B>
0
F(x)
– g(x)
< 0 в O(Xo)
<0
(по теореме о стабилизации знака)
А>B –противоречие => A<B
Вопрос №31
Бесконечно малые. Свойства бесконечно малых
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
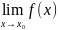= 0
Свойства бмв:
Сумма двух БМ в точке тоже является БМВ в этой точке
Произведение двух и более БМ в точке тоже является БМ в этой точке
Частное от деления бмв на функцию, предел которой ≠ 0, есть величина бм.
Вопрос №32
Бесконечно малые. Эквивалентные БМ. Теорема об эквивалентных БМ
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
= 0
Эквивалентные БМ:
Две БМ эквивалентны, если их предел = 1
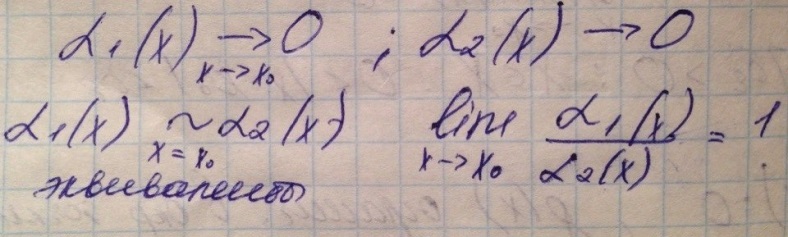
Теорема об эквивалентности БМ
Вопрос №33
Последовательность. Предел последовательности. Число е.
Последовательность – это функция натурального аргумента
Вопрос №34
Замечательные пределы
Первый замечательный предел
Пусть
х измеряется в радианах, тогда
= 1
Док-во: Для выполнения доказательства проверим функцию под знаком lim на четность.
(четная)
Т.к. функция является четной, то доказательство выполняется в I четверти, с использованием окружности единичного радиуса.
π/2
Sin x ===
=
Tg
x ===
SΔ AOC < S сек AOC < SΔAOD
SΔ
AOC =
*
OA = sin x *1 =
SΔ
AOD =
*OA
=
S
сек
AOC =
=
D
C
X
0 x
B
A
OA = 1
До множим все три части двойного неравенства на 2:
Sin
x < x <
Поделим все 3 части на sin x: и поскольку sin x в I четверти «+», то знаки двойного неравенства сохранятся
1<
1<
Выполним предельный переход в точу 0:
1
<
Т.к. нет такой величины, которая одновременно была бы и больше и меньше 1, то естественно, что первый замечательный lim =1
Ч.т.д.
2-ой
замечательный предел
n
= e
N=1
(1+
)1
= 2
N=2
(1+
)2
= 2, 25
N=3
(1+
)3
= 2, 35
n→∞ e = 2,71826…
Вопрос №35
Теорема о связи функции, имеющей конечный предел и БМ
Вопрос №36
БМ и ББ. Теорема о связи ББ и БМ
Бесконечно малая и бесконечно большая величины:
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
= 0
Функция f(x) называется бесконечно большой величиной в точке х0 принадл. R U ±∞, если = ∞
Теорема о связи бесконечно малых и бесконечно больших величин:
1. Пусть f(x)
является бмв в точке х0, тогда
является ббв в этой точке
Пусть f(x) является ббв в точке х0, тогда является бмв в этой точке
