
- •Вопрос №1
- •Вопрос №2 Арифметическое пространство. Линейные операции с арифметическими векторами
- •Вопрос №3 Матрицы. Линейные операции над матрицами и их свойства
- •Умножение на число
- •Вопрос №4 Транспонирование матриц. Определитель и его свойства
- •Вопрос №5 Умножение матриц. Свойства умножения
- •Вопрос №6 Обратная матрица. Необходимое и достаточное условие существования обратной матрицы
- •Вопрос №7 Линейная независимость элементов линейного пространства. Свойства линейной независимости
- •Вопрос №16 Скалярное произведение векторов. Свойства скалярного произведения. Угол между векторами
- •Вопрос №17 Скалярное произведение векторов. Необходимое и достаточное условие ортогональности векторов
- •Вопрос №38 Непрерывность числовой ф-ии одной переменной в точке. Точки разрыва, классификация точек разрыва
- •Вопрос №47 Производные и дифференциалы высших порядков
- •Вопрос №48 Теорема Ферма
- •Вопрос №49 Теорема Коши. Правило Лопиталя (без док-ва)
- •Вопрос №50 Теорема Лагранжа. Формула конечных приращений
- •Вопрос №53 Экстремумы ф-ии. Достаточное условие экстремума
- •Вопрос №54 Экстремумы ф-ии. Необходимое условие экстремума
Вопрос №1
Линейное пространство. Аксиомы линейного пространства.
Набор элементов(а,b,c…) называется линейным пространством таких, что на них введены несколько операций(сложение а+b=c, умножение на число L*a=d)
Операции должны подчиняться след. аксиомам:
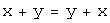 ,
сложение коммутативно;
,
сложение коммутативно;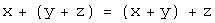 ,
сложение ассоциативно;
,
сложение ассоциативно;существует единственный нулевой элемент
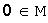 такой,
что
такой,
что  ,
, 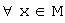 ;
;для каждого элемента существует единственный противоположный элемент
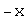 такой,
что
такой,
что 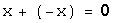 ,
,
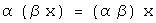 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;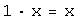 ,
;
,
;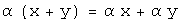 ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;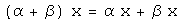 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Вопрос №2 Арифметическое пространство. Линейные операции с арифметическими векторами
Если на плоскости ввести систему координат, каждому вектору будет соотв. пара чисел (координат вектора). — вектор а (а1;а2).
ОПР: Арифметическим и n-мерным вектором называется любая последовательность из n чисел (а1 … аn ) или вектор n с его координатами. (а1 … аn ) – координаты вектора.
ОПР: Суммой двух векторов называют вектор, координаты которого равны сумме соответствующих координат этих векторов.
Свойства: 1. a+b= b+a. 2. (a+ b)+ c= a+ (b+ c). 3. Нулевым вектором будет называться вектор, у которого все координаты – нули: a(0, …, 0)=0, a+ 0= a. 4. Вектор с координатами (-a1, -a2, …, -an) будет называться противоположным вектору а, а+ (-а)= 0.
ОПР: Под произведением вектора на число будем подразумевать вектор, координаты которого умножены на данное число. С * вектор а = (са1,са2,…,саn)
Свойства: 1. k(a+ b)= ka+ kb а и b векторы. 2. (k+m)a= ka+ ma a – вектор. 3. k(la)= (kl)a a – вектор. 5. 1a= a, a – вектор.
Вопрос №3 Матрицы. Линейные операции над матрицами и их свойства
Матрица –это набор чисел записанных в таблицу состоящую из m строк и n столбцов
Линейные операции над матрицами и их свойства:
Сложение Свойства сложения:
А + В = В + А.
(А + В) + С = А + (В + С) .
Если О – нулевая матрица, то А + О = О + А = А
Умножение на число
Свойства умножения матрицы на число:
(km)A=k(mA).
k(A + B) = kA + kB.
(k + m)A = kA + mA.
3. Перемножение матриц.
Число столбцов первого множителя должно равняться числу строк второго
Вопрос №4 Транспонирование матриц. Определитель и его свойства
Транспонированной матрицей назовем такую матрицу, у которой строки матрицы заменены на столбцы
Определителем матрицы называется число, которое получается при сложении произведений элементов матрицы, взятых либо с «+», либо с « - » свойства:
Определитель равен нулю, если матрица содержит 0 строку (столбец)
Опр.матрицы равен 0, если она содержит одинак. Стр и столб
Определитель матрицы равен определитель транспонированной матрицы
Определитель матрицы изменит знак, сли поменять стр и стлб
Если стр(стлб) определит. Матр. Представляет собой сумму двух чисел, то определитель равен сумме двух определителей
Если стр(стлб) определит.кратен некоторому числу, это число можно вынести за знак опредеителя
Опр.матрицы не изм., если к любой стр(стлб) матрицы добавить др.строку(стлб) матрицы, умноженную на конст, не равн.0
