15 Слайд§5.3. Преобразование Лапласа

Аналогично Z-преобразованию в дискретном случае в непрерывном времени имеется преобразование, которое позволяет по функции действительного переменного найти некоторый ее образ, который будет находиться во взаимно однозначном соответствии с прообразом. Это L-преобразование или преобразование Лапласа:

, (5.3.1)

где – изображение Лапласа функции f, L-изображение или преобразование Лапласа;

– начальная функция или оригинал.

Рассмотрим 2 примера таких преобразований:

§5.5. Учет факторов в марковских моделях

пусть вероятность перехода между произвольными i-м и j-м состояниями может быть описана некоторой функцией, т.е.

, (5.5.1)

где U и V – m-мерные векторы факторов для состояний i и j соответственно.

Рассмотрим изменение вероятностей переходов при малом изменении компонент данных m-мерных векторов:

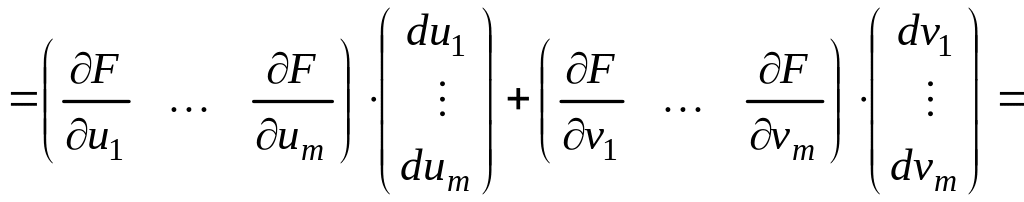
. (5.5.2)

Рассмотрим простейший случай, когда изменению могут быть подвергнуты лишь l-е компоненты векторов при неизменности остальных. Тогда

. (5.5.3)

Пусть при этом значение не изменилось, т.е.

. (5.5.4)

Естественно предположить, что это может иметь место при пропорциональном изменении факторов, при этом коэффициент пропорциональности

. (5.5.5)

С учетом (5.5.4) соотношение (5.5.3) перепишется так:

. (5.5.6)

Соотношение (5.5.6) положим в основу гипотезы 5.5.1, дополнительно сформулируем еще гипотезу 5.5.2 и докажем теорему 5.5.1, которая позволит ограничить класс функций вероятностей от факторов.

Гипотеза 5.5.1

Вероятности не меняются при пропорциональном изменении факторов, т.е.