Глава 4. Процессы Маркова в дискретном времени

§4.1. Основные понятия

2 слайд.Процессы Маркова относятся к случайным, или стохастическим процессам, под которыми понимается некоторая последовательность случайных переменных (состояний), которые соответствуют определенным значениям времени t [9, c.23]. Случайные переменные, как и значение времени t, могут задаваться дискретно или непрерывно. Такой процесс может быть описан с помощью условных вероятностей

3 Слайд

Итак, пусть имеется r возможных состоянияй и, следовательно, квадратная матрица переходных вероятностей, о которой говорилось уже выше

, (4.1.1)

Элементы , составляющие матрицу P, представляют собой вероятности перехода из состояния i в состояние j за один момент времени – шаг процесса. Поэтому (4.1.1) можно записать в виде

, (4.1.2)

при этом для произвольных .

Если же нас интересуют вероятности перехода из состояния i в состояние j, допустим, за шага, то рассуждаем следующим образом. Вероятность перехода из состояния i в состояние j через состояние может быть подсчитана по формуле полной вероятности

, (4.1.3)

что в матричном виде представляет собой

.

Распространяя вышеприведенные рассуждения на любое t, можно убедиться, что

, (4.1.4)

где . При этом t, как правило, конечно, хотя в целом ряде случаев будут делаться выводы и для .

4 слайд. Регулярные цепи Маркова

Матрица переходных вероятностей называется регулярной, если при некотором n все элементы матрицы отличны от 0.

Теорема 4.2.1

Пусть – переходная матрица, не содержащая нулевых элементов, и e – наименьший элемент P. Пусть – один из столбцов матрицы P, имеющий максимальную компоненту и минимальную компоненту (имеется в виду для данного вектора), и пусть и соответственно –максимальная и минимальная компоненты вектора PX. Тогда и .

5 Слайд Доказательство

Образуем вектор , элементами которого будут и величин . Пусть, например, вектор X представляет собой 1-й столбец матрицы Р, и его наименьшим элементом будет . Тогда соотношение между векторами X и Y будет таким:

. (4.2.1)

Далее запишем произведение PX и оценим его, используя (4.2.1):

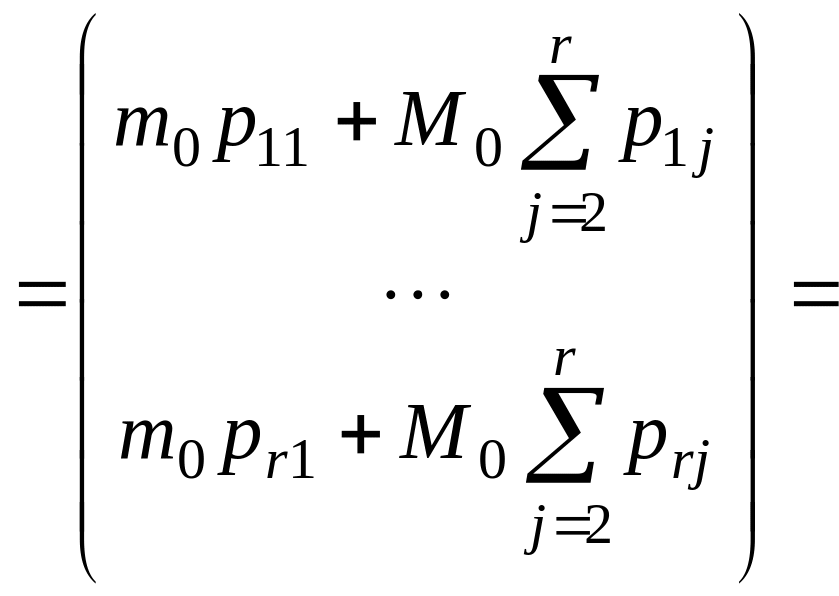
. (4.2.2)

Таким образом, в соответствии с соотношением (4.2.2) имеем

.

6 Слайд

Из .при и следует , что и требовалось доказать.

7 Слайд

Теорема

Если P – регулярная матрица, то

1. степени при стремятся к так называемой вероятностной матрице A;

2. каждая из строк матрицы A представляет собой один и тот же вероятностный вектор , называемый также неподвижным

3. все компоненты вектора  положительны.

;

8 Слайд

Доказательство

Применим теорему 4.2.1 к исходной матрице с положительными элементами. То есть будем брать последовательно каждый из r векторов , из которых эта матрица состоит, и оценивать результативные столбцы PX. Затем в качестве исходной будет использоваться матрица P, а в качестве векторов X – столбцы матрицы . На третьем шаге в качестве исходной будет использоваться все та же матрица P, а в качестве векторов X – столбцы матрицы и т. д. Наконец, на n-м шаге в качестве исходной будет использоваться все та же матрица P, а в качестве векторов X – столбцы матрицы . Так как для каждого из столбцов будем иметь соотношения и , то для каждого столбца матрицы значение максимального элемента будет убывать, а значение минимального – возрастать, при этом они будут оставаться положительными. Записав последовательность соотношений (4.2.6), получим

;

;

…

при ,

что завершает доказательство.