23. Исключение систе­матических погрешно­стей путем введения по­правок.

В ряде случаев систематические погреш­ности могут быть вычис­лены и исключены из ре­зультата измерения. Для этого используются по­правки.

Поправка C_j – величина, одноименная измеряемой, которая вводится в результат измерения с целью исключе­ния составляющих систематической погрешности θ_j.

При – j-я составляющая систематической погрешности полностью уст­раняется из результата измерения.

Поправки определяются экс­периментально или в результате специальных теоретических ис­следований. Они задаются в виде таблиц, графиков или формул. Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множе­ство поправок. При этом вследствие ограниченной точности опре­деления поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется ста­тистически – средним значением поправки С и СКО S_С. При ис­правлении результата путем введения поправок С_j, где j = 1, 2,..., m, по формуле дисперсия исправленного результата

где S_н² – оценка дисперсии неисправленного результата; S²_cj – оценка дисперсии j-й поправки. Как видно, с одной стороны, уточ­няется результат измерения, а с другой – увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти опти­мум.

Пусть при измерении постоянной величины Q получено (рис.7.1) значение , где – оценка среднего арифме­тического неисправленного результата измерений; t_р – коэффи­циент Стьюдента.

После введения поправки С ± t_рS_с результат измерения

, где

Максимальные доверительные значения погрешности результа­та измерения до и после введения поправки равны соответственно

Поправку имеет смысл вводить до тех пор, пока Δ₁ < Δ₂. Отсюда следует, что

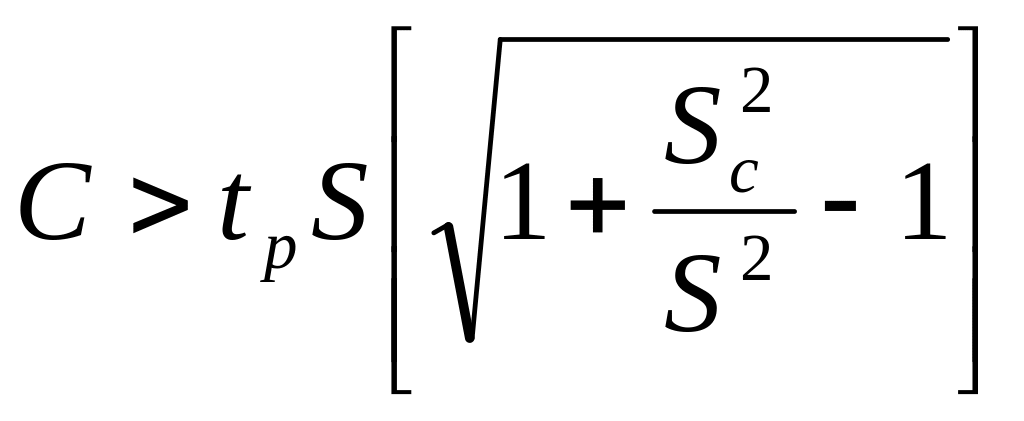
Если S_С/S << 1, то, раскладывая уравнение в степенной ряд, получим С > 0,5 S_c²/S² • Из этого неравенства видно, что если оцен­ка среднего квадратического отклонения поправки S_c→0, то по­правку имеет смысл вводить всегда.

В практических расчетах погрешность результата обычно выра­жается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смыс­ла.

24. Статистические критерии оценки нормальности распределения.

В качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используются критерии согласия. Известен целый ряд критериев согласия, предложенных разными авторами. Наибольшее распространение в практике получил критерий Пирсона (критерий хи–квадрат). Идея этого метода состоит в контроле отклонений гистограм­мы экспериментальных данных от гистограммы с таким же чис­лом интервалов, построенной на основе распределения, совпадение с которым определяется. Использование критерия Пирсона возможно при большом числе измерений (n > 50) и заключается в вычислении величины ² (хи – квадрат):

(8.1)

где n_j, N_j – экспериментальные и теоретические значения частот в i-м интервале разбиения; m – число интервалов разбиения; Р_i – значения вероятностей в том же интервале разбиения, соот­ветствующие выбранной модели распределения;

При n → ∞ случайная величина имеет распределение .Пирсо­на с числом степеней свободы v = m–1–r, где r – число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Если бы выбранная модель в центрах всех т столбцов совпадала с экспериментальными данными, то все т разностей (n_i – N_i) были бы равны нулю, а, следовательно, и значение критерия также было бы равно нулю. Таким образом, есть мера суммарного от­клонения между моделью и экспериментальным распределением.

Методика определения соответствия экспериментального и принятого законов распределения заключается в следующем:

• определяют оценки среднего арифметического значения и СКО ;

• группируют результаты многократных наблюдений по интер­валам длиной h, число которых определяют так же, как и при построении гистограммы;

• для каждого интервала разбиения определяют его центр х_i0 и подсчитывают число наблюдений n_i, попавших в каждый интервал;

• вычисляют число наблюдений для каждого из интервалов, теоретически соответствующее выбранной аналитической модели распределения. Для этого сначала от реальных середин интервалов х_i0 производят переходи нормированным серединам

z_i = (х_i0 – )/S_х .

По найденному значению f(z_i) определяют ту часть N_i, имею­щихся наблюдений, которая теоретически должна быть в каждом из интервалов N_i=nh f(z_i)/S_х, где n – общее число наблюдений;

• если в какой-либо интервал теоретически попадает меньше пяти наблюдений, то в обеих гистограммах его соединяют с сосед­ним интервалом. После этого определяют число степеней свободы v = m–1–r, где m – общее число интервалов. Если было произве­дено укрупнение, то m – число интервалов после укрупнения;

• по формуле 8.1 определяют показатель разности частот ;

• выбирают уровень значимости критерия q. Он должен быть небольшим, чтобы была мала вероятность, совершить ошибку пер­вого рода. По уровню значимости и числу степеней свободы v по табл. 8.1 находят границу критической области такую, что Р{ > } = q.

Вероятность того, что полученное значение превыша­ет , равна q и мала. Поэтому, если оказывается, что > , то гипотеза о совпадении экспериментального и теоретического законов рас­пределения отвергается. Если же < , то гипотеза принимается.

Чем меньше q, тем больше значение (при том же числе сте­пеней свободы v), тем легче выполняется условие < и прини­мается проверяемая гипотеза. Но при этом увеличивается вероят­ность ошибки второго рода. В связи с этим нецелесообразно при­нимать 0,02 q 0,01.