СОДЕРЖАНИЕ

Введение

1. Прямые измерения

1.1 Однократные измерения

1.2 Многократные измерения

2. Косвенные измерения

3. Измерение неэлектрической физической величины

Список использованной литературы

Введение

Магнитоэлектрические приборы для измерения малых токов – миллиамперметры представляют собой в простейшем случае измерительный механизм, обмотка которого присоединена непосредственно к внешним зажимам. Поэтому при включении прибора в цепь измеряемый ток идет по его обмотке. В этом случае изменение температуры окружающей среды не вызывает дополнительной температурной погрешности, т. к. изменение сопротивления медной обмотки не влияет на ток, который определяется главным образом сопротивлением приемника энергии.

Большинство амперметров магнитоэлектрической системы представляют собой измерительные механизмы, снабженные шунтом. У таких приборов изменение температуры окружающей среды вызывает изменение сопротивления медной обмотки, а сопротивления шунта остается неизменным, т. к. он изготовляется из манганина. Это приводит к перераспределению токов в параллельных ветвях прибора, изменению шунтирующего множителя и, следовательно, к дополнительной погрешности от температуры около 4% при изменении температуры на 10 °C.

Для уменьшения температурной погрешности прибора уменьшают температурный коэффициент ветви измерительного механизма, что обеспечивается включением в эту ветвь добавочного резистора из манганина. Добавочные резисторы применяются у амперметров классов точности 1; 1,5 и 2,5. амперметры более высоких классов точности имеют более сложные схемы температурной компенсации.

При выполнении работы использовался миллиамперметр М42305 класс точности 2,5; дополнительные погрешности влияния влажности и температуры соответственно δ_вл = ±1%, δ_т=±1,5%.

1. Прямые измерения.

1.1 Однократные измерения.

Методика обработки результатов прямых однократных измерений применима при выполнении следующих условий: составляющие погрешности известны, случайные составляющие распределены по нормальному закону, а неисключенные систематические, заданные своими границами - равномерно. Составляющими погрешности прямых однократных измерений являются:

• погрешности СИ, рассчитываемые по их метрологическим характеристикам;

• погрешность используемого метода измерений, определяемая на основе анализа в каждом конкретном случае;

Если последние две составляющие не превышают 15% погрешности СИ, то за погрешность результата однократного измерения принимают погрешность используемого СИ.

При однократном измерении показание прибора I=95 мА

△_∑=│△_си│+∑│△_доп│

△_∑=2,5%+1%+1,5%=5%.

Результат измерения: I=95±5% мА.

1.2 Многократные измерения.

При многократном измерении получена серия из 30 результатов измерений Х_i; i  (1…30). Эти результаты занесены в таблицу:

Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10	Х11	Х12	Х13	Х14	Х15
100	99	97	95	100	96	95	97	96	95	96	97	95	99	96
Х16	Х17	Х18	Х19	Х20	Х21	Х22	Х23	Х24	Х25	Х26	Х27	Х28	Х29	Х30
96	97	98	99	100	96	98	100	99	97	100	96	98	100	98

Последовательность обработки результатов измерений, произведенная по методике [1], включает следующие этапы:

• Доказательство отсутствия или незначительности систематической погрешности. Вычисление среднего арифметического значения 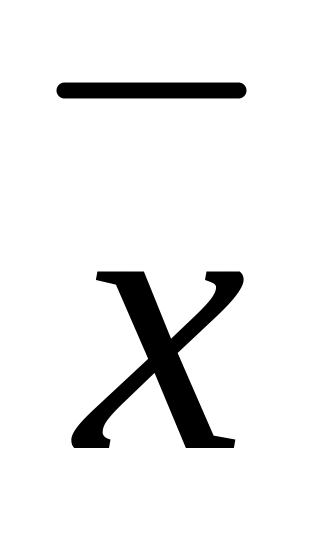по формуле 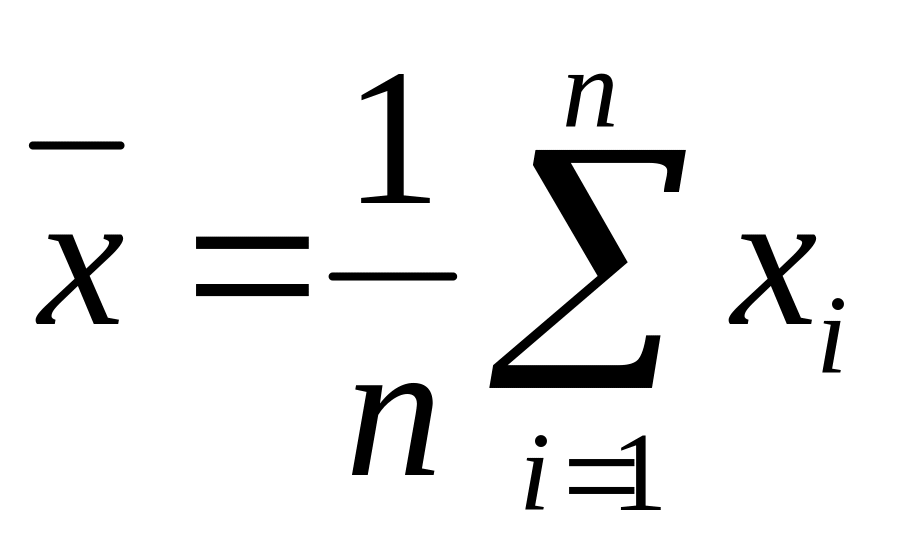(1).

• Вычисление выборочного СКО σ от значения погрешности измерения по формуле .

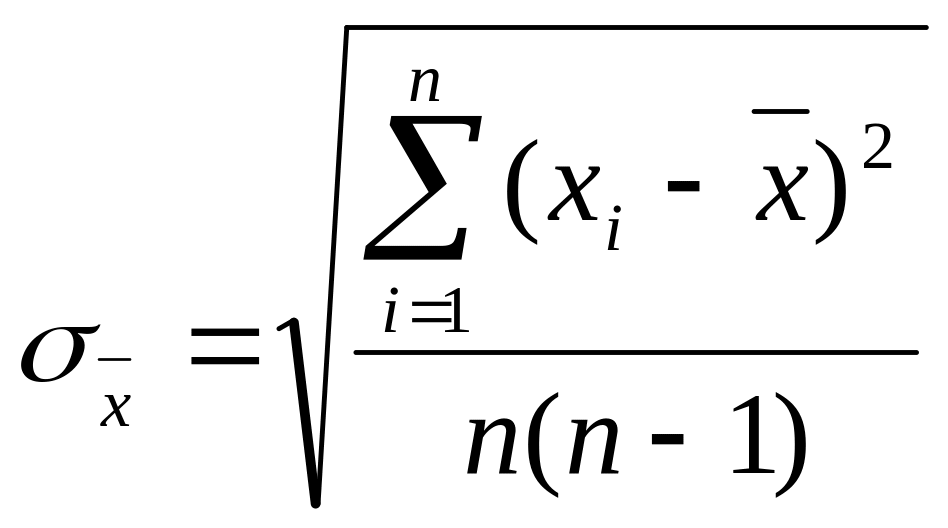• Выявление ошибочных результатов.

• Определение закона распределения случайной составляющей.

• Определение стандартного отклонения среднего арифметического

• При заданном значении доверительной вероятности Р и числе измерений n по таблицам определяем коэффициент Стьюдента t_p.

Нахождение границ доверительного интервала для случайной погрешности J= /

• Окончательный результат.

Обработка результатов для n≤30, n=15.

Вычисление среднего арифметического значения по формуле

=96,87 мА

Найдем точечную оценку дисперсии

D(x) = 3,27 мА

Для получения характеристики рассеивания результатов вокруг среднего арифметического значения в абсолютных единицах используют среднее квадратичное отклонение

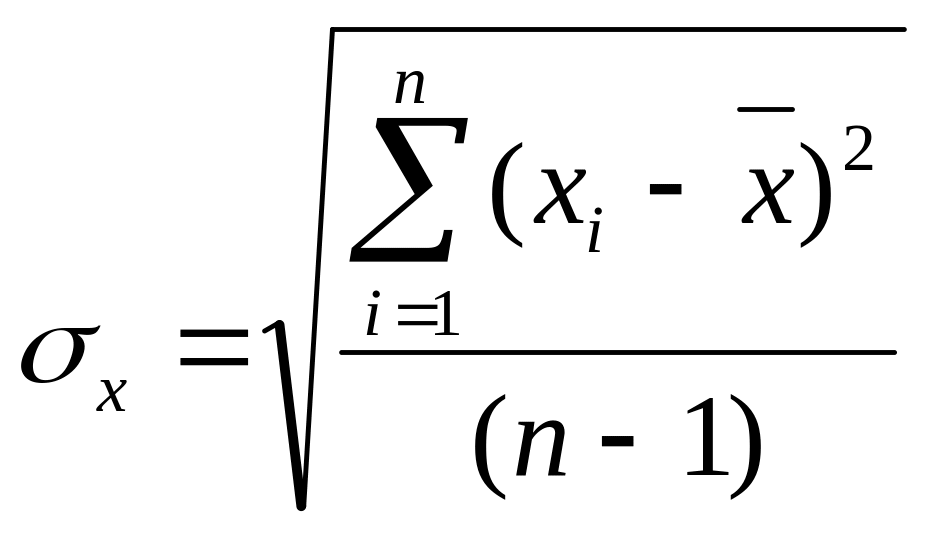
σ_х=1,81мА

Вычислим выборочное СКО σ от значения погрешности измерения по формуле .

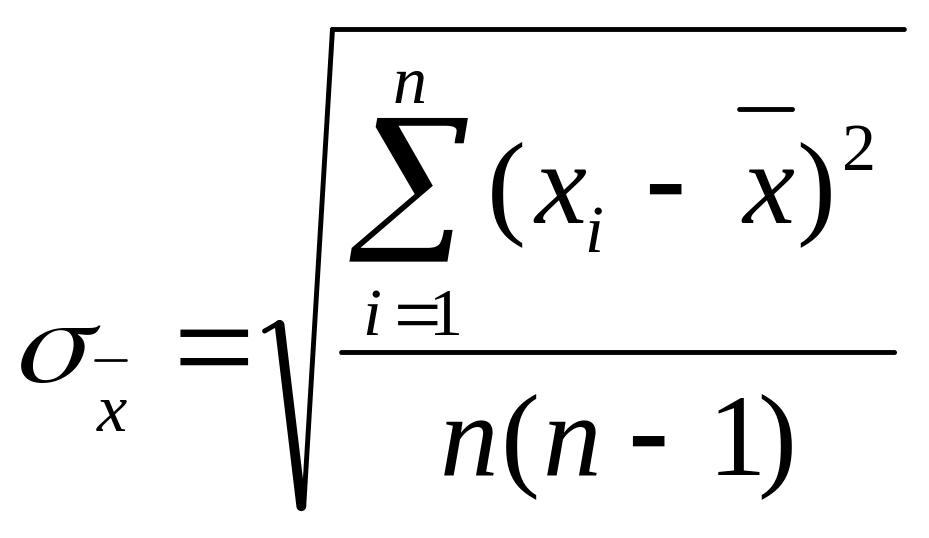= 0,47 мА

Выявим ошибочные результаты:

Так как n≤30, то для выявления ошибки применим критерий Романовского.

Для этого вычислим отношение и полученное значение β сравним с теоретическим β_т – при выбираемом уровне значимости Р₁ = 0.01, Р₂=0,05.

= 96,87 мА

σ = 1,81 мА

β ≈ 0,48

при Р=0,95 β_т =2,64,при Р=0,99 β_т =2,90

Так как β < β_т, ошибочных результатов нет.

Определение закона распределения случайной составляющей.

Для оценки закона распределения используем относительную величину СКО – коэффициент вариации:

= 1,81/96,87=0.019

Так как ≤ 0.33,…,0.35 можно считать, что распределение случайной величины подчиняется нормальному закону.

По заданным доверительным вероятностям Р=0,95 и Р=0,99 с учётом n=15 определим коэффициент Стьюдента t_p.

t_p1= 2.13

t_p2=1,75

Рассчитаем интервалы по формуле:

J= /

При Р=0,95 J=96,87±2,13×1,81/

J₁=97,87 мA, J₂=95,87 мA

При Р=0,99 J=96,87±1,75×1,81/

J₁=97,69 мA, J₂=96,05 мA

Рассчитаем Е=t× ,

Е₁= 3,86 мА,

Е₂= 3,17 мА.

Т.к. при Р=0,95 и Р=0,99 не более n разностей │ │ превосходит Е, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Результат измерения

при Р=0,95 Х=96,87±3,86 мА

при Р=0,99 Х=96,87±3,17 мА

Обработка результатов для n=30

Вычисление среднего арифметического значения по формуле

=97,5 мА

Найдем точечную оценку дисперсии

D(x) = 3,086 мА

Для получения характеристики рассеивания результатов вокруг среднего арифметического значения в абсолютных единицах используют среднее квадратичное отклонение

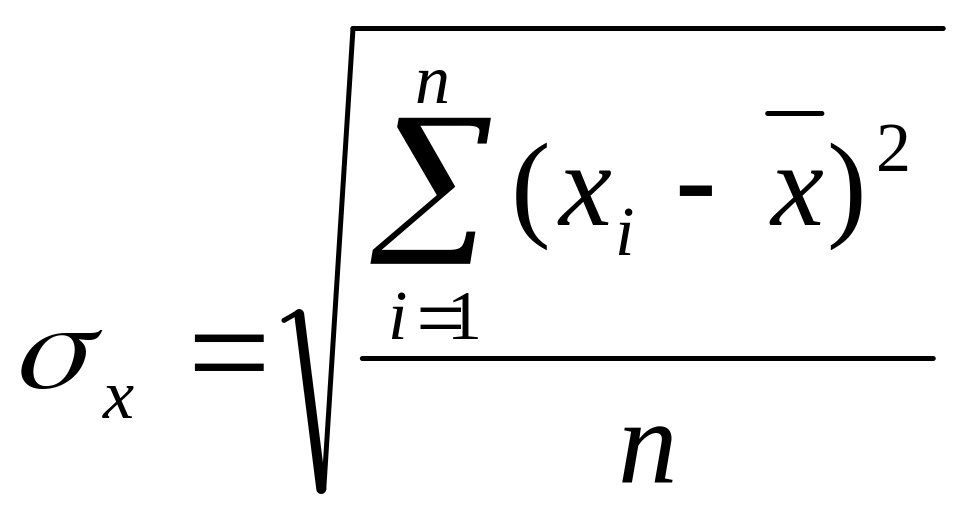
σ_х=1,73мА

Вычислим выборочное СКО σ от значения погрешности измерения по формуле .

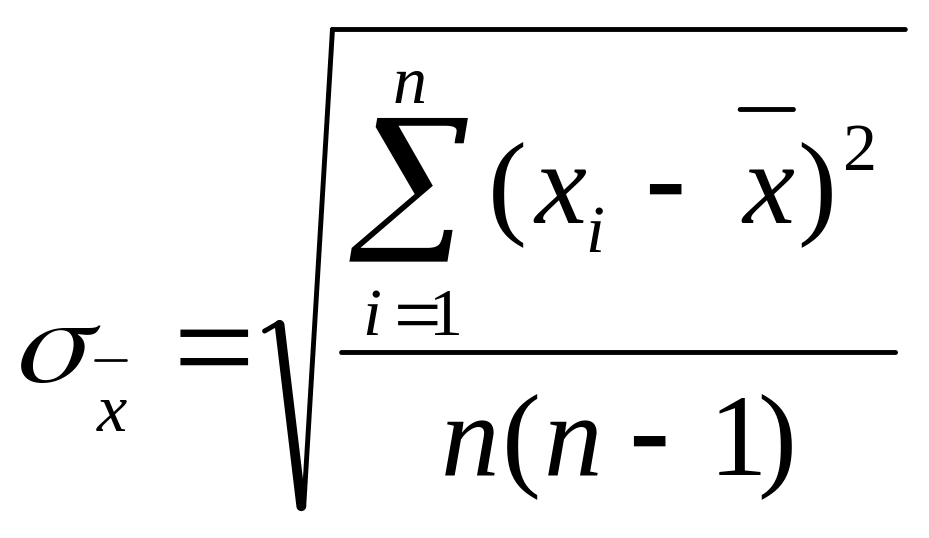= 0,32 мА

Выявим ошибочные результаты:

Так как n≥30, то для выявления ошибки применим критерий 3σ.

Для этого вычислим отношение .

= 97,48 мА

σ = 3,077 мА

= 0,52 мА

3σ = 9,231 мА

Так как < 3σ , ошибочных результатов нет.

Определение закона распределения случайной составляющей.

Для оценки закона распределения используем относительную величину СКО – коэффициент вариации:

= 1,73/97,5=0.018

Так как ≤ 0.33,…,0.35 можно считать, что распределение случайной величины подчиняется нормальному закону.

По заданным доверительным вероятностям Р=0,95 и Р=0,99 с учётом n=15 определим коэффициент Стьюдента t_p.

t_p1= 2.04

t_p2=1,70

Рассчитаем интервалы по формуле:

J= /

При Р=0,95 J=96,87±2,04×1,73/

J₁=96,86 мA, J₂=98,14 мA

При Р=0,99 J=96,87±1,7×1,73/

J₁=96,96 мA, J₂=98,04 мA

Рассчитаем Е=t× ,

Е₁= 3,53мА,

Е₂= 2,94 мА.

Т.к. при Р=0,95 и Р=0,99 не более n разностей │ │ превосходит Е, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Результат измерения

при Р=0,95 Х=97,5±3,53м А

при Р=0,99 Х=97,5±2,94 мА