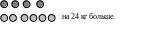3. Методика обучения решению задач

Тема: Обучение решению простых задач на сложение и вычитание

План:

1. Роль задач в начальном курсе математики (записать ответ на вопрос в тетрадь для лекций).

1. Обучение решению простых задач:

а) раскрывающих смысл действий сложения и вычитания;

б) на увеличение (уменьшение) числа на несколько единиц;

в) на разностное сравнение;

г) с неизвестным слагаемым;

д) с неизвестным уменьшаемым;

е) с неизвестным вычитаемым.

3. Анализ видов задач с теоретико-множественной точки зрения.

Рекомендательная литература

1. Гребенникова Н.Л. Ознакомление первоклассников с задачей // Начальная школа.– 1990. – № 10. – С. 34-37.

2. Истомина Н.Б. Первые шаги в формировании умения решать задачи // Начальная школа. – 1981. – № 11. – С. 40-42.

3. Царева С.Е. Приемы первичного анализа задачи // Начальная школа. – 1985. – № 9. – С. 46-49.

4. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач // Начальная школа. – 1985. – № 10. – С. 37-39.

В начальном курсе математики большую роль играют задачи. Они выполняют функцию не только самостоятельного объекта изучения, но и важного средства, с помощью которого младшие школьники осваивают математические понятия. В зависимости от количества действий, с помощью которых решается задача, различают задачи простые (в одно действие) и составные (в два и более действий) в начальных классах вводятся 25 видов только простых задач, каждый из которых имеет свои методические особенности. Поэтому решение обычно является «камнем преткновения» для младших школьников. В связи с этим, рассмотрим данный вопрос более подробно.

Что значит решить задачу? На этот вопрос отвечают, как правило, следующим образом: «Решить задачу – это значит найти правильный ответ». Но это не совсем так решить задачу, это значит:

- разобраться в условии задачи, выделить входящие в нее величины, определить, какие из них известны, а какую надо найти;

- выяснить, как между собой эти величины связаны;

- на основе этого правильно выбрать арифметическое действие;

- записать соответствующий пример, вычислить его и записать ответ.

Как видим, решение задачи включает в себя следующие элементы: а) анализ условия задачи, выделение известных величин и той, которую надо найти; б) краткая запись условия задачи; в) разбор задачи, составление плана решения (в составных задачах); г) запись решения; д) проверка решения.

Виды задач в 1 классе

В 1 классе четырехлетней начальной школы дети знакомятся со следующими видами простых задач:

Вид задачи	Пример данного вида задачи
1. На нахождение суммы	У Саши было 6 тетрадей в клетку и 2 в линейку. Сколько всего тетрадей было у Саши?
2. На нахождение остатка	У Саши было 8 тетрадей. 2 тетради он сдал учителю. Сколько тетрадей у него осталось?
3. На увеличение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради больше. Сколько всего тетрадей было у Саши?

4. На уменьшение числа на несколько единиц

У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради меньше. Сколько всего тетрадей было у Саши?

Задачи на нахождение суммы

Задачи на нахождение суммы раскрывают конкретный смысл действия сложения. Поэтому на подготовительном этапе работы над этим видом задачи необходимо постоянно оперировать с предметными множествами, делая упор на операцию объединения множеств. Приведем пример такой работы.

- Положи слева 5 красных кружочков, а справа – 3 синих кружочка. Придвинь синие кружочки к красным (при этом делается жест объединения синих кружочков с красными). Больше стало кружочков или меньше? (Больше.) Сколько всего стало кружочков? (8.) Каким действием это узнаем? (Сложением.)

В дальнейшем осуществляется переход предметных действий с кружочками к их моделям, которые вычерчиваются в тетради (размер кружочка – одна клеточка, интервал между ними тоже одна клеточка). В этом случае объединение множеств ребенок осуществляет мысленно и фиксирует это объединение на чертеже в виде стрелочки.

Для того, чтобы лучше разобраться в условии задачи, выделить входящие в нее величины, выполняется краткая запись условия, которая предшествует выбору арифметического действия и записи решения задачи. Для данного вида задач традиционной является следующая форма краткой записи условия (рассмотрим ее на примере приведенного выше текста задачи):

Пояснение обозначений: К. – тетрадей в клетку, Л. – тетрадей в линейку.

Однако величины, входящие в условие задачи, и отношения между ними более наглядно отображаются в краткой записи условия, которая выполнена в виде следующих схем:

а) схема в форме полоски:

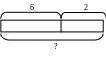
б) схема в форме отрезка:

Использование таких схем больше помогает детям правильно выбрать нужное арифметическое действие для решения задачи.

Решение задачи на данном этапе записывают следующим образом:

6 + 2 = 8 (т.)

Ответ: 8 тетрадей.

Задачи на нахождение остатка

Д анный вид задачи раскрывает конкретный смысл действия вычитания. Методика работы с такими задачами похожа на предыдущий вид, только вместо операции объединения множеств используется операция удаления части множества. Традиционная форма краткой записи условия выглядит так:

?

Задачи на увеличение и уменьшение числа на несколько единиц.

В основе правильного решения этих видов задач лежит понимание смысла отношений «больше на», «меньше на». Так, например, если тетрадей в клетку – 6, а в линейку на 2 больше, то это значит, что в линейку столько же, сколько в клетку, и еще 2. на схеме это отношение оформляется так:

Проверочные задания по теме «Решение задач»

Реши задачи:

1. В одной тарелке 5 яблок, а в другой – 4 яблока. Сколько яблок в двух тарелках?

2. У Саши было 7 марок. 2 марки он подарил другу. Сколько марок осталось у Саши?

3. В одной вазе – 6 цветов, а в другой – на 2 больше. Сколько цветов во второй вазе?

4. В гараже было 8 легковых машин, а грузовых – на 3 меньше. Сколько грузовых машин было в гараже?

5. На столе лежат 5 ложек, а вилок на 2 больше, чем ложек. Сколько вилок лежат на столе?

6. Сшили 9 платьев, а блузок на 3 меньше, чем платьев. Сколько сшили блузок?

7. Антону 7 лет, а его сестре на 2 года меньше. Сколько лет сестре Антона?

8. К озеру идут 5 уток, а утят на 4 больше, чем уток. Сколько утят идут к озеру?

9. Феде 10 лет, а Петя моложе Феди на 3 года. Сколько лет Пете?

10. На берегу 7 пингвинов, а на льдине на 3 пингвина меньше. Сколько пингвинов на льдине?

Решение простых задач

Во 2 классе продолжают решать простые задачи. В дополнение к тем, которые были представлены в 1 классе, приведем еще несколько видов.

Вид задачи	Особенности работы над данным видом
На нахождение неизвестного слагаемого	Пример данного вида задачи: «В гараже было 5 грузовых и несколько легковых машин. Всего в гараже было 8 машин. Сколько легковых машин было в гараже?» Решение задач данного вида основывается на знании и умении применять следующее правило: «чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое». Однако опыт показывает, что дети не всегда осознанно используют это правило и решение данного вида задач часто усваивают формально. Для преодоления этой трудности могут оказать помощь следующие средства: 1) Построение моделей в виде отрезков. Построим модель для приведенной выше задачи:
	2) Обращение к понятиям «часть» и «целое». В этом случае рассуждения ребенка по приведенной выше модели выглядят следующим образом: «Известно целое (8 м.) и часть (5 м.). Чтобы найти часть, нужно из целого вычесть другую часть». 3) Одновременное решение задач на нахождение неизвестного слагаемого и задач на нахождение суммы, т.к. они являются взаимно обратными задачами
На разностное сравнение	Различают два вида задач на разностное сравнение, которые отличаются друг от друга вопросом: 1) задачи с вопросом «на сколько больше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько легковых машин было больше, чем грузовых?); 2) задачи с вопросом «на сколько меньше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько грузовых машин в гараже было меньше, чем легковых?) Трудность состоит в том, что, несмотря на разные опорные слова в вопросах этих задач, обе они решаются действием вычитания. Дети же, ориентируясь на слово «больше», иногда для решения выбирают действие сложения. в установлении правильных отношений между величинами в задачах на разностное сравнение поможет «метод следов». Его суть состоит в следующем. На столе выкладывается в верхнем ряду 5 красных кружочков, а в нижнем ряду – 8 синих кружочков: затем кружочки убираются парами (по одному из каждого ряда) до тех пор, пока в верхнем ряду все кружочки не закончатся. В ходе этого процесса наглядно видно, почему задача решается действием вычитания:

Тема: Методика обучения решению простых задач на умножение и деление

План:

1. Самостоятельно изучить по учебникам (подобрать примеры) конкретный смысл операций умножения и деления с теоретико-множественной точки зрения и методика обучения решению простых задач следующих видов:

- задачи на нахождение суммы одинаковых слагаемых;

- задачи на деление по содержанию и делению на равные части;

- задачи на нахождение неизвестных компонентов действий умножения;

- задачи на увеличение в несколько раз;

- задачи на уменьшение в несколько раз;

- задачи на кратное сравнение.

2. По учебникам математики М2 [15] и М3 [16] классов сделать анализ задач вышеуказанных видов.

Рекомендательная литература

1. Царева С.Е. Проверка выбора действий при решении простых задач // Начальная школа. – 1981. – № 9. – С. 35-37.

2. Царева С.Е. Приемы первичного анализа задачи // Начальная школа. – 1985. – № 9. – С. 46-49.

3. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач (нахождение неизвестных компонентов) // Начальная школа.– 1985.– № 10. – С. 37-39.

Так как центральной темой 3 класса является умножение и деление, то новые виды простых задач связаны с этими действиями. Остановимся на методике решения трех видов простых задач: 1) на увеличение числа в несколько раз; 2) на уменьшение числа в несколько раз; 3) на кратное сравнение.

Вид задачи	Текст задачи	Краткая запись условия, разбор, запись решения задачи
На увеличение числа в несколько раз	В гараже находится 4 грузовых машины, а легковых – в 3 раза больше. Сколько легковых машин в гараже?	Краткая запись решения 1 вариант: Г. – 4 м. Л. - ?, в 3 раза больше. 2 вариант: В основе разбора задачи лежит понимание смысла отношения «в несколько раз больше»: если грузовых машин – 4, а легковых – в 3 раза больше, то это значит, что легковых машин – 3 раза по 4. Этому отношению соответствует умножение. Запись решения 4 · 3 = 12 (м.).
На уменьшение числа в несколько раз	в гараже находится 12 грузовых машин, а легковых – в 3 раза меньше. Сколько легковых машин в гараже?	Краткая запись решения 1 вариант: Г. – 12. Л. - ?, в 3 раза меньше. 2 вариант: Разбор задачи В основе разбора задачи лежит понимание смысла отношения «в несколько раз меньше. Этому отношению соответствует действие деление. Запись решения 12 : 3 = 4 (м.).
На кратное сравнение	В гараже находится 4 грузовых машины и 12 легковых. Во сколько раз легковых машин в гараже больше, чем грузовых?	Краткая запись решения 1 вариант: в ? раз больше 2 вариант: Разбор задачи в основе разбора задачи лежит понимание смысла отношения «во сколько раз (больше) меньше? Этому отношению соответствует действие деление. Запись решения 12 : 4 = 3 (м.).

Тема: Простые и составные задачи

План:

1. Система простых задач начального курса математики (различные классификации: традиционный, подход П.М. Эрдниева, подход Н.Б. Истоминой).

1. Содержание упражнений подготовительного этапа при переходе от простых задач к составным.

2. Первое знакомство с составной задачей (ответ подготовить в виде плана-конспекта).

Рекомендательная литература

1. Свечников А.А. Решение математических задач в 1–3-х классах. – М., 1976. – С. 45–52.

1. Истомина Н.Б. Работа над составной задачей // Начальная школа. – 1988. – № 2. – С. 44-49. (Подготовительный этап).

2. Уткина Н.Г. Составные задачи в 1-м классе // Изучение трудных тем по математике в 1–3-х классах. – М., 1982. – С. 45-52.

3. Гребенникова Н.Л. Опоры-перфокарты в обучении решению задач // Начальная школа. – 1992. – № 7-8. – 38 с.

4. Смирнова С.И. Использование чертежа при решении простых задач // Начальная школа. – 1998. – № 5. – С. 53-58.

Во 2 классе четырехлетней начальной школы впервые вводятся составные задачи (напомним, что составными называются задачи, которые решаются в два и более действий). Рассмотрим методику поэтапной работы с такими задачами:

Подготовительный этап. На этом этапе работа ведется с парами простых задач, таких, что ответ первой задачи является одним из данных чисел второй задачи. Приведем пример пары таких задач:

1) У Саши было 6 тетрадей в клетку и 2 тетради в линейку. Сколько всего тетрадей было у Саши?

2) У Саши было 8 тетрадей. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

В этой паре ответ первой задачи (8 тетрадей) является данным условием второй задачи.

На основе пары таких простых задач легко ввести составную задачу: У Саши было 6 тетрадей в клетку и 2 тетради в линейку. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

Основная трудность в решении таких задач состоит в том, что ребенок Перове действие выполняет в уме, а общее решение записывает так:

8 – 3 = 5 (т.)

На вопрос: «Откуда взялось число 8? Ведь его в условии задачи не было», чаще всего дети дают такой ответ «Но ведь 6 и 2 будет 8».

Решение пар простых задач позволяет предупредить эту ошибку и помочь детям осознать тот факт, что одним действием такую задачу решить нельзя.

Этап знакомства с составной задачей. Дети знакомятся с составной задачей на примере двух вариантов задач:

1) составной задачи, в которой первое действие является простой задачей на уменьшение числа на несколько единиц, а второе – простой задачей на нахождение суммы («В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»);

2) составной задачи, в которой первое действие является простой задачей на нахождение суммы, а второе – простой задачей на нахождение остатка («Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»). На примере этих задач рассмотрим методические особенности работы с ними.

Процесс работы над задачей состоит из следующих основных этапов:

1) Краткая запись условия задачи, которая помогает лучше разобраться в ее содержании.

2) Разбор задачи, в ходе которого выявляются отношения между данными и искомой величиной, осуществляется выбор арифметического действия.

3) Запись решения задачи и полученного ответа.

Для первого варианта составной задачи эти этапы будут выглядеть следующим образом.

Текст задачи:

«В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»

Краткая запись условия

Разбор задачи:

- Что известно в задаче? (В первой тарелке 5 груш, а во второй на 2 груши меньше.)

- Какой главный вопрос в задаче? (Сколько груш в двух тарелках?)

- Можем ли мы сразу ответить на этот вопрос? (Нет.)

- Что для этого нужно знать (Сколько груш в каждой тарелке.)

- Сколько груш в первой тарелке? (5.)

- А что сказано про вторую? (В ней на 2 груши меньше.)

- Как узнать, сколько груш во второй тарелке? (Нужно из 5 вычесть 2.)

- Как потом узнать, сколько груш в двух тарелках? (Нужно к тому, что получится в первом действии, прибавить 5.)

- Верно. Итак, сколько действий в этой задаче? (Два.)

- Какое первое действие? (Из 5 вычтем 2.)

- Что мы узнаем, выполнив это действие? (Сколько груш во второй тарелке?)

- Что будем делать во втором действии? (К результату первого действия прибавим 5.)

- Что узнаем, выполнив это действие? (Сколько груш в двух тарелках.)

Запись решения задачи

(с пояснением)

1) 5 – 2 = 3 (г.) – было во 2 тарелке.

2) 5 + 3 = 8 (г.) – всего в двух тарелках.

Ответ: 8 груш.

Приведем пример реализации данных этапов для второго варианта составной задачи.

Текст задачи:

«Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»

Краткая запись условия

Вырезали – 6 ф. и 4 ф.

Повесили – 3 ф.

Осталось - ?

Разбор задачи

(синтетический способ)

- Что известно в задаче? (Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку.)

- Какой главный вопрос в задаче? (Сколько флажков осталось?)

- Зная, что вырезали 6 красных флажков и 4 синих, что мы можем узнать? (Сколько всего флажков вырезали.)

- Каким действием это узнаем? (Сложением.)

- Зная, сколько флажков вырезали, и что 3 флажка из них повесили на елку, что мы можем найти? (Сколько флажков осталось.)

- Каким действием найдем? (Вычитанием.)

Запись решения задачи

(составлением выражения)

(6 + 4) – 3 = 7 (ф.)

Ответ: 7 ф.

Как видим, на примере, двух вариантов составных задач представлены основные способы краткой записи условия, разбора и записи решения, которые используются во 2 классе. Рассмотрим их более подробно.

Краткая запись условия задачи начинает вводиться постепенно. Сначала для этого используются начальные буквы опорных слов, а затем и сами опорные слова: «Было», «подарил», «продали», «улетело», «осталось» и т.д. При работе над вторым вариантом задачи использована такая краткая запись условия. Однако она не всегда помогает отразить реальные отношения между данными и искомыми величинами в задаче. Поэтому при решении как простых, так и составных задач мы рекомендуем использовать краткую запись в виде схем, чертежей, отрезков. Пример такой краткой записи условия приведен в первой задаче.

В начальной школе используются два основных способа рассуждений при разборе задачи: аналитический и синтетический. Аналитический способ более подробный, он начинается с главного вопроса задачи и постепенно восходит к величинам, данным в условии. Он используется, как правило, при освоении нового вида задачи. При синтетическом способе рассуждений мысль движется в обратном порядке: от условия задачи к главному вопросу. Этот способ является менее развернутым и пользуется, как правило, при разборе уже знакомых задач.

После разбора задачи переходят к записи ее решения. В настоящее время в начальной школе наиболее распространенной является запись решения по действиям с кратким пояснением результата действия. Этот способ показан в первой задаче. Освоив запись решения по действиям, можно переходить к записи решения способом составления выражения. В выражении выполняются те же действия, но они представлены в свернутом виде, поэтому данный способ требует более высокого уровня умения решать задачи.

Тема: Обучение решению задач с пропорциональными величинами

План:

1. Упражнения в учебнике, приводящие к понятиям «прямая и обратная зависимость».

1. Формирование представлений о прямопропорциональной и обратнопропорциональной зависимости.

2. Простые задачи с тройкой пропорциональных величин и особенности работы с ними.

3. Составные задачи с пропорциональными величинами:

а) составные задачи, содержащие в качестве одной из простых задачи с тройкой пропорциональных величин;

б) задачи на нахождение четвертого пропорционального;

в) задачи на пропорциональное деление;

г) задачи на нахождение неизвестного по двум разностям.

Рекомендательная литература

1. Скаткин Л.Н., Жигалкина Т.К. Обучение решению задач с пропорциональными величинами.– М.: Просвещение, 1979. – 32 с.

1. Гребенникова Н.Л. Решение задач на зависимость величин различными способами // Начальная школа. – 1999. – № 2. – С. 45-49.

2. Казько Е.С. Работа с текстом задачи с пропорциональными величинами // Начальная школа.– 1998. – № 5.– С. 70-74.

В начальных классах дети знакомятся с тройками пропорциональных величин: цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и т.д. С этими величинами можно особо выделить 3 вида составных задач: на нахождение четвертого пропорционального; на пропорциональное деление; на нахождение неизвестного по двум разностям. Первый из этих видов вводится в 3 классе, а второй и третий – в 4 классе, рассмотрим особенности работы над задачами на нахождение четвертого пропорционального с величинами: цена, количество, стоимость.

На подготовительном этапе в ходе решения простых задач отрабатываются правила нахождения одной из величин по двум другим, пропорциональным ей: например, как найти цену, зная стоимость и количество. После этого можно перейти к решению составных задач.

Текст задачи

За 5 метров ткани заплатили 40 рублей. Сколько стоят 7 метров такой же ткани?

Краткая запись условия

Запись условия задач с пропорциональными величинами оформляется в виде таблицы:

Цена	Количество	Стоимость
Одинаковая	5 м 7 м	40 р. ?

Разбор

На начальном этапе разбор таких задач осуществляется аналитическим способом:

- Что известно в задаче? (Что за 5 метров ткани заплатили 40 рублей.)

- Что еще дано в условии задачи? (7 метров такой же ткани.)

- Какой главный вопрос задачи? (Сколько стоят 7 метров такой же ткани?)

- Можем ли мы сразу ответить на главный вопрос задачи? (Нет.)

- Что для этого нужно знать? (Для того, чтобы найти стоимость, нужно знать цену и количество.)

- Количество известно, а что сказано про цену? (Что она одинаковая.)

- Как же найти цену по стоимости и количеству? (Нужно стоимость (40 р.) разделить на количество (5 м.))

- Найдя цену, как узнаем стоимость 7 метров ткани? (Цену умножим на количество метров.)

Запись решения

1 способ – по действиям с пояснением:

1) 40 : 5 = 8 (р.) – стоит 1 м ткани.

2) 8 · 7 = 56 (р.) – стоят 7 м ткани.

Ответ: 56 рублей

2 способ – составлением выражения:

40 : 5 · 7 = 56 (р.)

Ответ: 56 рублей

В дальнейшем от аналитического способа разбора можно переходить к синтетическому, а краткую запись условия можно сделать более компактной:

5 м – 40 р.

7 м - ?

Наиболее сложными задачами, которые изучаются в з классе, являются задачи, связанные с пропорциональными величинами. Рассмотрим решение этих задач на примере задачи на нахождение неизвестных по двум разностям и задачи на пропорциональное деление.

Вид задачи	На пропорциональное деление
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы. Всего в магазин привезли 120 кг овощей. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия
Разбор задачи	Аналитический способ разбора: Что известно в задаче? Что нужно узнать в задаче? Можем ли мы сразу ответить, сколько килограммов картофеля привезли в магазин? (Нет.) Что для этого нужно знать? (Массу одного ящика и количество ящиков.) Количество ящиков известно, а как можно найти массу одного ящика? (Общую массу разделить на общее количество ящиков.) Как приведем общее количество ящиков? (К 6 прибавим 4.) Узнав массу одного ящика, как найдем массу всего картофеля? (Массу одного ящика умножим на количество ящиков с картофелем.) Как узнать массу всей свеклы? (Массу одного ящика умножим на количество ящиков со свеклой.) Как можно другим способом узнать массу всей свеклы? (из общей массы вычесть массу картофеля.)
Запись решения	Запись решения по действиям с пояснением: 6 + 4 = 10 (ящ.) – привезли всего. 120 : 10 = 12 (кг) – масса одного ящика. 12 · 6 = 72 (кг) – привезли картофеля. 12 · 4 = 48 (кг) – привезли свеклы. Ответ: 72 кг и 48 кг.
Вид задачи	Нахождение неизвестных по двум разностям
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы, причем картофеля привезли на 24 кг больше, чем свеклы. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия	Из этой наглядной записи хорошо видно, что 24 кг картофеля находятся в 2 ящиках.
Разбор задачи	Синтетический способ: Что известно в задаче? Что нужно узнать в задаче? Почему картофеля оказалось в магазине на 24 кг больше (Потому, что ящиков с картофелем было больше.) На сколько ящиков больше? (на 2.) Какой вывод из этого можно сделать? (Что 24 кг картофеля находится в 2 ящиках.) Зная это, как найти массу одного ящика с картофелем? (Нужно 24 кг разделить на 2.) Как теперь найти массу картофеля и массу свеклы? (Массу одного ящика умножить на количество ящиков.)
Запись решения	Запись решения с предварительной постановкой вопросов: На сколько ящиков картофеля привезли больше, чем свеклы? 6 – 4 = 2 (ящ.) Какова масса одного ящика с овощами? 24 : 2 = 12 (кг) Сколько килограммов картофеля привезли в магазин? 12 · 6 = 72 (кг) Сколько килограммов картофеля привезли в магазин? 12 · 4 = 48 (кг) Ответ: 72 кг картофеля и 48 кг свеклы.

Тема: Методика работы над задачами на движение

План:

1. Подготовительные упражнения к теме (на нахождение расстояния, промежутка времени, скорости).

1. Простые задачи с тройкой пропорциональных величин: скорость – время – расстояние, последовательность работы над вопросом.

2. Задачи на движение:

а) подготовительные составные задачи на движение одного или двух тел;

б) задачи на движение в противоположных направлениях и новые понятия, возникающие в связи с их решением (скорость сближения – при встречном движении и скорость удаления – при движении друг от друга);

в) движение в одном направлении.

Рекомендательная литература

1. Лысенкова С.Н. Когда легко учиться. – М., 1985.

1. Рудницкая В.Н. Формирование у школьников понятия «скорость» // Начальная школа. – 1993. – № 1. – С. 40-43.

3. Холомкина А.И. Решение задач на движение // Начальная школа. – 1983. – № 3. – С. 46-49.

«Скорость» – одна из наиболее трудных тем курса математики начальной школы. Опыт показывает, что решение даже несложных арифметических задач, содержащих зависимость между скоростью, путем и временем движения, часто вызывает затруднения у многих учащихся, в том числе и у имеющих в целом неплохую математическую подготовку. Еще больше трудностей возникает у учащихся при решении составных задач (на движение вдогонку, на движение тел в противоположных направлениях и пр.).

Покажем другой подход к введению понятия «скорость».

Основой подхода является рассмотрение и сравнение движений нескольких (двух или трех) предметов. Поставив перед учащимися задачу – определить, какой из предметов движется быстрее (при заданных условиях), и произведя соответствующие вычисления, легко подведем учащихся к пониманию необходимости введения особой величины (скорости), являющейся характеристикой быстроты движения, и ее единиц.

Для первоначального ознакомления учащихся со скоростью выделяем два урока. Первый урок начинаем с краткого вступления. Учитель говорит: «Вы уже знакомы с некоторыми важными величинами – длиной, массой, временем, научились их измерять. Сегодня мы познакомимся с новой величиной, многие из вас слышали ее название – скорость. Чтобы понять, что такое скорость, решим задачу: «Петя на лыжах пробежал 30 м за 10 с. а Федя – 30 м за 15 с. Кто из мальчиков бежал быстрее?»

Наверное, многие из вас сообразят, кто бежал быстрее. Выскажите свое мнение. Почему вы так думаете?

Давайте разберемся. Федя пробежал то же расстояние, что и Петя, но затратил больше времени. Чтобы ответить на вопрос задачи о том, кто из мальчиков бежал быстрее, надо узнать, сколько метров пробегал каждый из них в одну секунду:

30:10=3 30:15=2

Итак, Петя пробегал 3 м в каждую секунду, а Федя – только 2 м в ceкунду. Говорят так: «Петя бежал с большей скоростью, чем Федя. Скорость Пети была 3 метра в секунду, а скорость Феди - 2 метра в секунду».

Метр в секунду – это единица скорости.

Ее обозначают так: м/с. Есть и другие единицы скорости, например, километр в секунду (км/с), километр в час (км/ч), метр в минуту (м/мин).

Как же найти скорость, если известны длина пути и время? Какое действие надо выполнить?

Чтобы найти скорость, надо длину пути разделить на время.

Если ракета летит со скоростью 9 км/с, то это значит, что в каждую секунду она пролетает 9 км. Если машина идет со скоростью 85 км/ч, то это значит, что она проходит 85 км в каждый час. Если черепаха движется со скоростью 5 м/мин, то это значит, что она проползает 5 м в каждую минуту.

Упражнения.

1. Объясните смысл предложения:

а) самолет летит со скоростью 950 км/ч;

б) улитка ползет со скоростью 6 м/ч;

в) плот плывет по реке со скоростью 4 км/ч;

г) человек идет со скоростью 5 км/ч.

2. Назовите скорость, с которой может идти пешеход, автобус, такси, электропоезд, лететь самолет.

3. Чему равна скорость движения:

а) меч-рыбы, если она в каждый час проплывает 100 км?

б) пчелы, если она в каждую секунду пролетает 7 м?

в) верблюда, если он в каждый час проходит 35 км?

г) космического корабля, если он в каждую секунду пролетает 8 км?

д) велосипедиста, если он в каждый час проезжает 18 км?

4. Вы знаете, что для определения массы используют прибор, который называют весы, для измерения длины используют линейку или рулетку, для измерения времени - часы. А каким прибором измеряют скорость?

Для измерения скорости используют прибор, который называют спидометром (от англ. speed – скорость). По показаниям спидометра узнайте и запишите скорость движения каждой машины:

5. За 6 ч, двигаясь без остановок, поезд прошел 498 км. Сколько километров проходил поезд в каждый час? С какой скоростью шел поезд?

6. Один велосипедист за 2 ч проехал 24 км, а другой за то же время – 26 км. Найдите скорость каждого велосипедиста. Скорость какого велосипедиста больше? Что значит скорость больше?

7. За 1 ч автомобиль прошел 60 км. Сколько километров он проходил в каждую минуту? Запишите скорость автомобиля, используя единицу скорости км/мин.

8. Я заметил в бинокль предмет, движущийся со скоростью 1000 м/мин. Выразите эту скорость в км/мин.

В течение следующих 3-4 уроков по известной учителю методике учащиеся решают задачи на определение пути по данным скорости и времени движения и на определение времени по двум другим известным величинам – пути и скорости.

После рассмотрения решения, каждой из этих задач полезно вслух проговорить выводы: 1) чтобы найти длину пути, надо время умножить на скорость; 2) чтобы найти время, надо длину пути разделить на скорость.

При решении задач на движение в средних классах учащиеся встречаются с большими трудностями - переводом скорости, данных в одних единицах, в другие единицы. Дело не в том, что соответствующее умение трудно сформировать. Этим надо специально заниматься, а в программе по математике для начальной школы этому вопросу не уделяется внимания и нужных видов упражнений в учебнике математики, естественно, нет. А определенную работу в этом направлении можно провести уже в начальных классах.

Предлагаем для тренировки несколько видов таких упражнений. Эти упражнения помогут научить учащихся переводить одни единицы в другие и будут способствовать развитию их мышления.

Упражнения.

1. Космический корабль летит со скоростью 8 км/с. Сколько километров он пролетит за 1 мин? Запишите скорость корабля в км/мин.

2. Машина прошла 150 км за 2 ч 30 мин. Найдите скорость машины и запишите ее в км/ч.

3. Велосипедист едет по дороге со скоростью 15 км/ч. Какое расстояние он проедет за 20 мин?

Решение. Покажем наиболее простой способ рассуждения. В 1 ч содержится 3 раза по 20 мин (60:20=3). Значит, 20 мин – это 1/3 часа. Так как каждый час велосипедист проезжает 15 км, то за 3 часа он проедет 5 км (15:3=5). Ответ. 5 км.

4. Человек идет по дороге со скоростью 4 км/ч. За какое время он пройдет 3 км?

Решение. По условию задачи человек проходит 4 км за 60 мин. Значит, 1 км он проходит за 15 мин (60:4= 15), а 3 км он пройдет за 45 мин (15·3=45).

Ответ. За 45 мин.

5. Стрекоза летит со скоростью 10 м/с. Сколько километров она пролетит за 1 ч?

Решение. В 1 ч содержится 3 600 с (60·60=3600). По условию задачи за 1 с стрекоза пролетает 10 м, а за час, т.е. за 3 600 с она пролетит в 3 600 раз большее расстояние, т.е. 10·3600=36000=36 километров.

Ответ. 36 км.

При обучении решению задач на движение двух тел в противоположных направлениях для предупреждения механического запоминания некоторыми учениками способа решения задачи полезно предлагать задачи, по сюжету и способу решения знакомые учащимся, но числовые данные подбирать так, чтобы формальный, заученный способ решения, примененный к таким задачам, привел бы учеников к ошибке или поставил их в тупик и они вынуждены были думать, рассуждать, искать правильное решение.

Примеры таких задач.

1. Два пешехода вышли одновременно навстречу друг другу из двух деревень. Скорость одного пешехода 5 км/ч, а другого 4 км/ч. Расстояние между деревнями 3 км. Какое расстояние будет между пешеходами через час после начала движения?

Решение. Через час от начала движения пешеход, идущий со скоростью 5 км/ч, пройдет 5 км. За это время он дойдет до деревни (до нее 3 км) и пройдет дальше еще 2 км. Второй пешеход за час дойдет до деревни (3 км) и пройдет еще 1 км. Значит, через час от начала движения расстояние между пешеходами будет 6 км (3+2+1=6).

Ответ. 6 км.

2. Из села в город на велосипеде выехал почтальон со скоростью 12 км/ч. В то же время навстречу ему из города в село вышел турист со скоростью 6 км/ч. Расстояние от села до города 9 км. Какое расстояние будет между ними через полчаса?

Решение. За полчаса почтальон проедет 6 км (12:2=6), а турист пройдет 3 км (6:2=3). Так как расстояние от села до города 9 км, то через полчаса после начала движения почтальон, пройдя 6 км, а турист 3 км, встретятся (6+3=9). В момент встречи расстояние между ними будет 0.

О т в е т. Расстояние равно 0.

Тема: Общий порядок работы над задачей

Выполнить задания:

1. Описание общего порядка работы над задачей.

2. Оформить решение задачи в тетради ученика.

3. Анализ традиционного и одного из альтернативных подходов при работе над задачей.

Рекомендательная литература

1. Свечников А.А. Решение математических задач в 1-3 классах. – М., 1976.

2. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – 288 с.

При работе над задачей можно руководствоваться рекомендациями статьи Царевой С.Е. Обучение решению задач // Начальная школа. – 1997. – № 11. – С. 93-98. Ниже приведен её краткий вариант.

Этапы решения задачи и приемы их выполнения