8.Схема Бернулли. Формула Бернулли. Локальная и интегральная теорема Муавра-Лапласа

Проводятся   опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью   (или не произойти — «неудача» —  ). Задача — найти вероятность получения ровно   успехов в опыте.

Решение:

Количество успехов — величина случайная, которая имеет биномиальное распределение.

Теперь рассмотрим эту задачу подробнее. Возьмём самый простой стохастический эксперимент с двухэлементным пространством элементарных событий. Одно назовём «успехом», обозначим «1», другое — «неудачей», обозначим «0».

Пусть вероятность успеха  , тогда вероятность неудачи  .

Рассмотрим новый стохастический эксперимент, который состоит в  -кратном повторении этого простейшего стохастического эксперимента.

Понятно, что пространство элементарных событий  , которое отвечает этому новому стохастическому эксперименту будет   (1),  . За  -алгебру событий   возьмём булеан пространства элементарных событий   (2). Каждому элементарному событию   поставим в соответствие число  . Если в элементарном событии   успех наблюдается   раз, а неудача —   раз, то  . Пусть  , тогда  . Также является очевидной нормированность вероятности:  .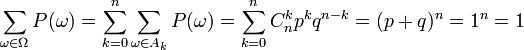

Поставив в соответствие каждому событию   числовое значение   (3), мы найдём вероятность  . Построенное пространство  , где Ω — пространство элементарных событий, определено равенством (1),  —  -алгебра, определена равенством (2), P — вероятность, определена равенством (3), называетсясхемой Бернулли для   испытаний.

Набор чисел   называется биномиальным распределением.

Теоремы Муавра-Лапласа. На практике приближенные формулы Муавра-Лапласа применяются в случае, когда pи q не малы , а npq>9.

Локальная теорема Муавра-Лапласа. Если вероятность появления события А в каждом из n  независимых испытаний равна одной и той же постоянной р=const (0<р<1), то вероятность   того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой:

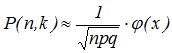, (4.8)

где: 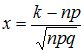  ,  -- кривая Гаусса.

Таблицы значений функции   даны в приложениях к учебникам по теории вероятностей

Интегральная теорема Муавра-Лапласа. Пусть вероятность появления события А в каждом из n (n→∞)независимых испытаний равна одной и той же постоянной р (0<р<1), то вероятность   того, что во всех этих испытаниях событие А появится не менее k₁ и не более k₂ раз, приближенно вычисляется формулой:

, (4.9)

где

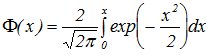 - функция Лапласа,

, 

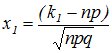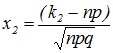
Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная - F(x)= F(-x).

9.Биномиальное распределение.

Биномиальное распределение — дискретное распределение вероятностей одной случайной величины   принимающей целочисленные значения   с вероятностями:

Данное распределение характеризуется двумя параметрами: целым числом   называемым числом испытаний, и вещественным числом     называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из   независимых испытаний, в каждом из которых может произойти "успех" с вероятностью   то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы   независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: 

Моменты:

• Математическое ожидание: 

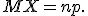
• Дисперсия: 

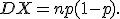
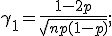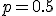• Асимметрия:   при   распределение симметрично относительно центра