6.Понятие дискретной случайной величины. Закон распределения дискретной одномерной случайной величины. Функция распределения f(X), ее свойства.

	Величина, которая в результате испытания может принять то или иное значение, заранее неизвестно какое именно, считается случайной.   Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.   Сотношение, устанавливающее связь мужду отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины.Если обозначить возможные числовые значения случайной величины Х через х1, х2, ..., хn,..., а через рi = Р(Х = хi) вероятность появления значения хi, то дискретная случайная величинаполностью определяется таблицей:
xi		х1	x2	...	xn
pi		p1	p2	...	pn

Таблица называется законом распределения дискретной случайной величины Х.

Дискретная случайная величина может быть задана функцией распределения.   Функцией распределения случайной величины Х называется функция F(х), выражающая вероятность того, что Х примет значение, меньшее чем х: F(x) = P(X < x) =  pi, где суммирование по хi < x

  Вероятность попадания случайной величины Х в промежуток от  до  выражается формулой 

Р( <= X < ) =F( ) - F()

Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора. При соблюдении известных условий (см. ниже) полностью определяет случайную величину.

Пусть дано вероятностное пространство  , и на нём определена случайная величина   с распределением  . Тогда функцией распределения случайной величины  называется функция  , задаваемая формулой:

.

То есть функцией распределения (вероятностей) случайной величины   называют функцию  , значение которой в точке   равно вероятности события  , то есть события, состоящего только из тех элементарных исходов, для которых  .

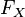•  непрерывна справа:^[1]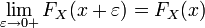

• 

•  не убывает на всей числовой прямой.

• .

• .

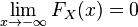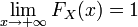• Распределение случайной величины   однозначно определяет функцию распределения.

• Верно и обратное: если функция   удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что   является её функцией распределения.

• По определению непрерывности справа, функция   имеет правый предел 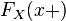  в любой точке 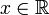 , и он совпадает со значением функции 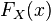  в этой точке.

• В силу неубывания, функция   также имеет и левый предел 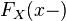  в любой точке  , который может не совпадать со значением функции. Таким образом, функция   либо непрерывна в точке, либо имеет в ней разрыв первого рода.